 |
MODFLOW 6
version 6.7.0.dev2
USGS Modular Hydrologic Model
|
 |
MODFLOW 6
version 6.7.0.dev2
USGS Modular Hydrologic Model
|
Functions/Subroutines | |
| subroutine, public | traverse_triangle (isolv, tol, texit, alpexit, betexit, itrifaceenter, itrifaceexit, alp1, bet1, alp2, bet2, alpi, beti) |
| Traverse triangular cell. More... | |
| subroutine, public | canonical (x0, y0, x1, y1, x2, y2, v0x, v0y, v1x, v1y, v2x, v2y, xi, yi, rxx, rxy, ryx, ryy, sxx, sxy, syy, alp0, bet0, alp1, bet1, alp2, bet2, alpi, beti) |
| Set coordinates to "canonical" configuration. More... | |
| subroutine, public | get_w (alp1, bet1, alp2, bet2, waa, wab, wba, wbb) |
| Compute elements of W matrix. More... | |
| subroutine, public | solve_coefs (alpi, beti) |
| Compute analytical solution coefficients depending on case. More... | |
| subroutine, public | step_analytical (t, alp, bet) |
| Step (evaluate) analytically depending on case. More... | |
| subroutine, public | find_exit_bary (isolv, itriface, itrifaceenter, alpi, beti, tol, texit, alpexit, betexit) |
| Find the exit time and location in barycentric coordinates. More... | |
| real(dp) function | fbary1 (bet) |
| Brent's method applied to canonical face 1 (gamma = 0) More... | |
| real(dp) function | fbary2 (bet) |
| Brent's method applied to canonical face 2 (alpha = 0) More... | |
| subroutine, public | get_t_alpt (bet, t, alp) |
| Given beta evaluate t and alpha depending on case. More... | |
| subroutine, public | get_bet_outflow_bary (vn1, vn2, betoutlo, betouthi) |
| Find outflow interval. More... | |
| subroutine, public | get_bet_soln_limits (beti, betsollo, betsolhi, ibettrend) |
| Find trend of and limits on beta from beta{t} solution. More... | |
| subroutine, public | soln_brent (itriface, betlo, bethi, tol, texit, alpexit, betexit) |
| Use Brent's method with initial bounds on beta of betlo and bethi. More... | |
| subroutine, public | soln_chand (itriface, betlo, bethi, tol, texit, alpexit, betexit) |
| Use Chandrupatla's method with initial bounds on beta of betlo and bethi. More... | |
Variables | |
| real(dp) | ca1 |
| real(dp) | ca2 |
| real(dp) | ca3 |
| real(dp) | cb1 |
| real(dp) | cb2 |
| Analytical solution coefficients. More... | |
| real(dp) | waa |
| real(dp) | wab |
| real(dp) | wba |
| real(dp) | wbb |
| Elements of the "velocity matrix," W. More... | |
| real(dp), dimension(2) | cv0 |
| real(dp), dimension(2) | cv1 |
| real(dp), dimension(2) | cv2 |
| "Canonical" velocity components at corners of triangular subcell More... | |
| integer(i4b) | icase |
| Case index for analytical solution. More... | |
| subroutine, public ternarysolvetrack::canonical | ( | real(dp) | x0, |
| real(dp) | y0, | ||
| real(dp) | x1, | ||
| real(dp) | y1, | ||
| real(dp) | x2, | ||
| real(dp) | y2, | ||
| real(dp) | v0x, | ||
| real(dp) | v0y, | ||
| real(dp) | v1x, | ||
| real(dp) | v1y, | ||
| real(dp) | v2x, | ||
| real(dp) | v2y, | ||
| real(dp) | xi, | ||
| real(dp) | yi, | ||
| real(dp) | rxx, | ||
| real(dp) | rxy, | ||
| real(dp) | ryx, | ||
| real(dp) | ryy, | ||
| real(dp), intent(inout) | sxx, | ||
| real(dp), intent(inout) | sxy, | ||
| real(dp), intent(inout) | syy, | ||
| real(dp) | alp0, | ||
| real(dp) | bet0, | ||
| real(dp) | alp1, | ||
| real(dp) | bet1, | ||
| real(dp) | alp2, | ||
| real(dp) | bet2, | ||
| real(dp) | alpi, | ||
| real(dp) | beti | ||
| ) |
| ryy | rotation matrix | |
| [in,out] | syy | skew matrix entries (top left, top right, bottom right) |
| beti | alpha and beta coefficients |
Definition at line 99 of file TernarySolveTrack.f90.


|
private |
Definition at line 505 of file TernarySolveTrack.f90.


|
private |
Definition at line 519 of file TernarySolveTrack.f90.


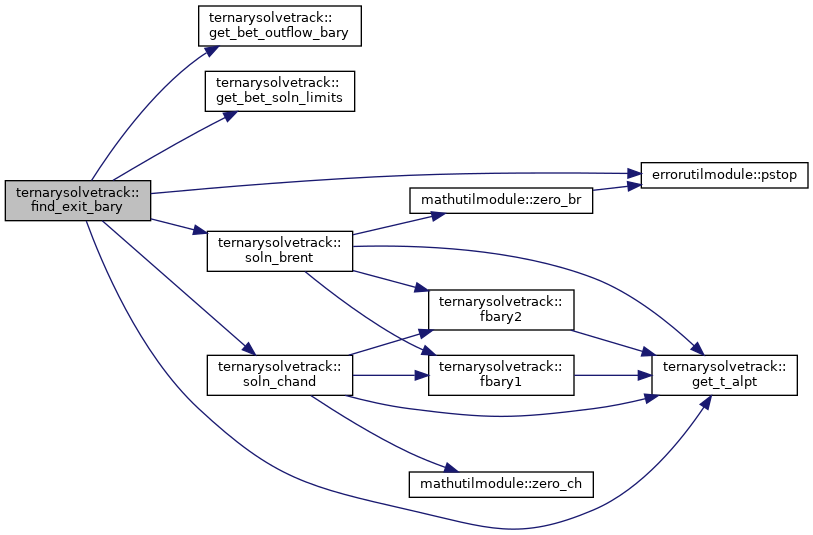
| subroutine, public ternarysolvetrack::find_exit_bary | ( | integer(i4b) | isolv, |
| integer(i4b) | itriface, | ||
| integer(i4b) | itrifaceenter, | ||
| real(dp) | alpi, | ||
| real(dp) | beti, | ||
| real(dp) | tol, | ||
| real(dp) | texit, | ||
| real(dp) | alpexit, | ||
| real(dp) | betexit | ||
| ) |
Definition at line 325 of file TernarySolveTrack.f90.

| subroutine, public ternarysolvetrack::get_bet_outflow_bary | ( | real(dp) | vn1, |
| real(dp) | vn2, | ||
| real(dp) | betoutlo, | ||
| real(dp) | betouthi | ||
| ) |
| subroutine, public ternarysolvetrack::get_bet_soln_limits | ( | real(dp), intent(in) | beti, |
| real(dp) | betsollo, | ||
| real(dp) | betsolhi, | ||
| integer(i4b), intent(inout) | ibettrend | ||
| ) |
| subroutine, public ternarysolvetrack::get_t_alpt | ( | real(dp), intent(in) | bet, |
| real(dp) | t, | ||
| real(dp) | alp | ||
| ) |
| subroutine, public ternarysolvetrack::get_w | ( | real(dp) | alp1, |
| real(dp) | bet1, | ||
| real(dp) | alp2, | ||
| real(dp) | bet2, | ||
| real(dp) | waa, | ||
| real(dp) | wab, | ||
| real(dp) | wba, | ||
| real(dp) | wbb | ||
| ) |
| bet2 | triangle face points |
| wbb | w matrix |
Definition at line 196 of file TernarySolveTrack.f90.

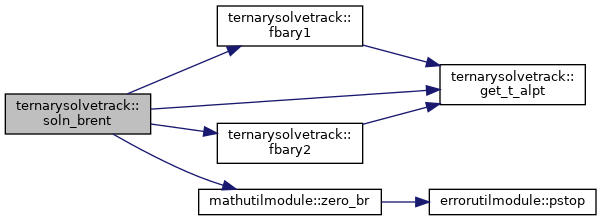
| subroutine, public ternarysolvetrack::soln_brent | ( | integer(i4b), intent(in) | itriface, |
| real(dp) | betlo, | ||
| real(dp) | bethi, | ||
| real(dp), intent(in) | tol, | ||
| real(dp) | texit, | ||
| real(dp) | alpexit, | ||
| real(dp) | betexit | ||
| ) |
Definition at line 684 of file TernarySolveTrack.f90.

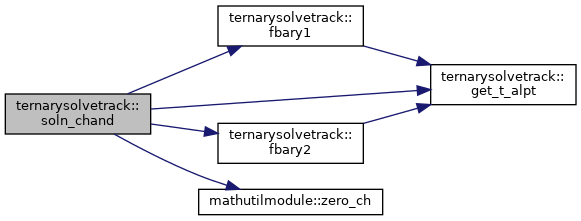
| subroutine, public ternarysolvetrack::soln_chand | ( | integer(i4b), intent(in) | itriface, |
| real(dp) | betlo, | ||
| real(dp) | bethi, | ||
| real(dp), intent(in) | tol, | ||
| real(dp) | texit, | ||
| real(dp) | alpexit, | ||
| real(dp) | betexit | ||
| ) |
Definition at line 714 of file TernarySolveTrack.f90.

| subroutine, public ternarysolvetrack::solve_coefs | ( | real(dp) | alpi, |
| real(dp) | beti | ||
| ) |
| subroutine, public ternarysolvetrack::step_analytical | ( | real(dp), intent(in) | t, |
| real(dp) | alp, | ||
| real(dp) | bet | ||
| ) |
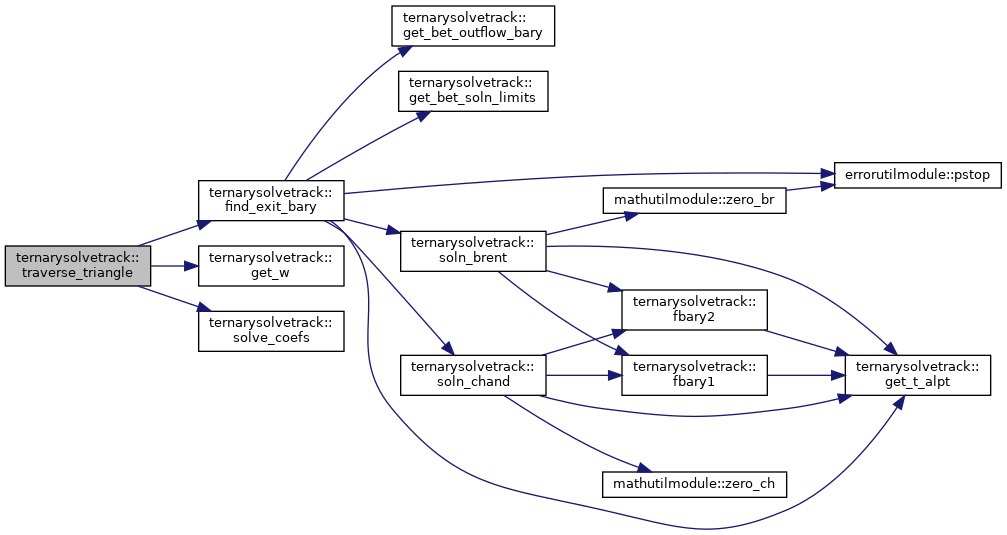
| subroutine, public ternarysolvetrack::traverse_triangle | ( | integer(i4b), intent(in) | isolv, |
| real(dp), intent(in) | tol, | ||
| real(dp), intent(out) | texit, | ||
| real(dp) | alpexit, | ||
| real(dp) | betexit, | ||
| integer(i4b) | itrifaceenter, | ||
| integer(i4b) | itrifaceexit, | ||
| real(dp) | alp1, | ||
| real(dp) | bet1, | ||
| real(dp) | alp2, | ||
| real(dp) | bet2, | ||
| real(dp) | alpi, | ||
| real(dp) | beti | ||
| ) |
| [in] | isolv | solution method |
| [in] | tol | solution tolerance |
| [out] | texit | time particle exits the cell |
| betexit | alpha and beta coefficients | |
| itrifaceexit | entry and exit faces | |
| beti | alpha and beta coefficients |
Definition at line 32 of file TernarySolveTrack.f90.

|
private |
Definition at line 24 of file TernarySolveTrack.f90.
|
private |
Definition at line 24 of file TernarySolveTrack.f90.
|
private |
Definition at line 24 of file TernarySolveTrack.f90.
|
private |
Definition at line 24 of file TernarySolveTrack.f90.
|
private |
Definition at line 24 of file TernarySolveTrack.f90.
|
private |
Definition at line 26 of file TernarySolveTrack.f90.
|
private |
Definition at line 26 of file TernarySolveTrack.f90.
|
private |
Definition at line 26 of file TernarySolveTrack.f90.
|
private |
Definition at line 27 of file TernarySolveTrack.f90.
|
private |
Definition at line 25 of file TernarySolveTrack.f90.
|
private |
Definition at line 25 of file TernarySolveTrack.f90.
|
private |
Definition at line 25 of file TernarySolveTrack.f90.
|
private |
Definition at line 25 of file TernarySolveTrack.f90.