|
MODFLOW 6
version 6.8.0.dev0
USGS Modular Hydrologic Model
|
 |
MODFLOW 6
version 6.8.0.dev0
USGS Modular Hydrologic Model
|
Functions/Subroutines | |
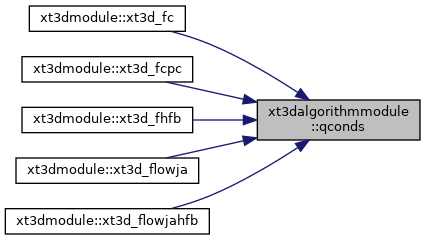
| subroutine | qconds (nnbrmx, nnbr0, inbr0, il01, vc0, vn0, dl0, dl0n, ck0, nnbr1, inbr1, il10, vc1, vn1, dl1, dl1n, ck1, ar01, ar10, vcthresh, allhc0, allhc1, chat01, chati0, chat1j) |
| Compute the "conductances" in the normal-flux expression for an interface (modflow-usg version). The cell on one side of the interface is "cell 0", and the one on the other side is "cell 1". More... | |
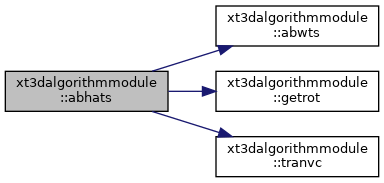
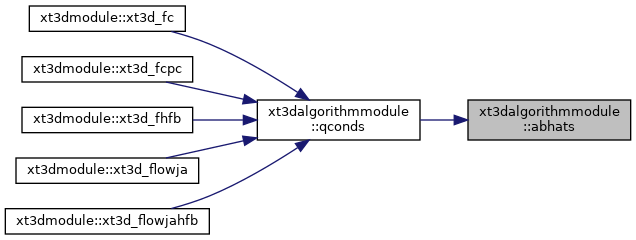
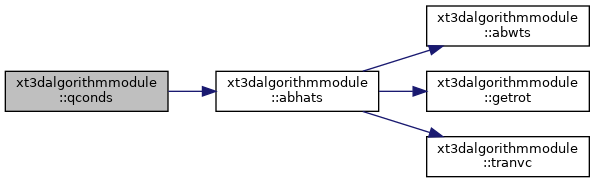
| subroutine | abhats (nnbrmx, nnbr, inbr, il01, vc, vn, dl0, dln, ck, vcthresh, allhc, ar01, ahat, bhat) |
| Compute "ahat" and "bhat" coefficients for one side of an interface. More... | |
| subroutine | getrot (nnbrmx, nnbr, inbr, vc, il01, rmat, iml0) |
| Compute the matrix that rotates the model-coordinate axes to the "(c, d, e)-coordinate" axes associated with a connection. More... | |
| subroutine | tranvc (nnbrmx, nnbrs, rmat, vc, vccde) |
| Transform local connection unit-vectors from model coordinates to "(c, d, e)" coordinates associated with a connection. More... | |
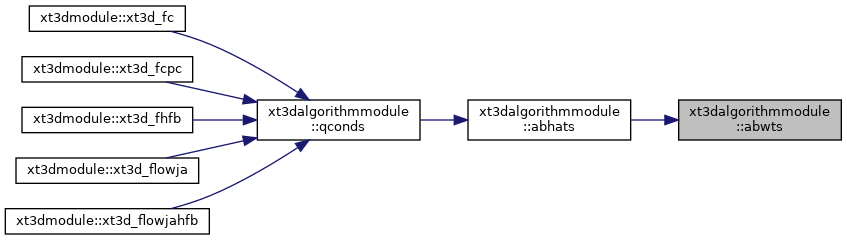
| subroutine | abwts (nnbrmx, nnbr, inbr, il01, nde1, vccde, vcthresh, dl0, dln, acd, add, aed, bd) |
| Compute "a" and "b" weights for the local connections with respect to the perpendicular direction of primary interest. More... | |
| subroutine xt3dalgorithmmodule::abhats | ( | integer(i4b) | nnbrmx, |
| integer(i4b) | nnbr, | ||
| integer(i4b), dimension(nnbrmx) | inbr, | ||
| integer(i4b) | il01, | ||
| real(dp), dimension(nnbrmx, 3) | vc, | ||
| real(dp), dimension(nnbrmx, 3) | vn, | ||
| real(dp), dimension(nnbrmx) | dl0, | ||
| real(dp), dimension(nnbrmx) | dln, | ||
| real(dp), dimension(3, 3) | ck, | ||
| real(dp) | vcthresh, | ||
| logical | allhc, | ||
| real(dp) | ar01, | ||
| real(dp) | ahat, | ||
| real(dp), dimension(nnbrmx) | bhat | ||
| ) |
Definition at line 127 of file Xt3dAlgorithm.f90.
| subroutine xt3dalgorithmmodule::abwts | ( | integer(i4b) | nnbrmx, |
| integer(i4b) | nnbr, | ||
| integer(i4b), dimension(nnbrmx) | inbr, | ||
| integer(i4b) | il01, | ||
| integer(i4b) | nde1, | ||
| real(dp), dimension(nnbrmx, 3) | vccde, | ||
| real(dp) | vcthresh, | ||
| real(dp), dimension(nnbrmx) | dl0, | ||
| real(dp), dimension(nnbrmx) | dln, | ||
| real(dp) | acd, | ||
| real(dp) | add, | ||
| real(dp) | aed, | ||
| real(dp), dimension(nnbrmx) | bd | ||
| ) |
nde1 = number that indicates the perpendicular direction of primary interest on this call: "d" (2) or "e" (3). vccde = array of connection unit-vectors with respect to (c, d, e) coordinates. bd = array of "b" weights. aed = "a" weight that goes on the matrix side of the 2x2 problem. acd = "a" weight that goes on the right-hand side of the 2x2 problem.
Definition at line 389 of file Xt3dAlgorithm.f90.
| subroutine xt3dalgorithmmodule::getrot | ( | integer(i4b) | nnbrmx, |
| integer(i4b) | nnbr, | ||
| integer(i4b), dimension(nnbrmx) | inbr, | ||
| real(dp), dimension(nnbrmx, 3) | vc, | ||
| integer(i4b) | il01, | ||
| real(dp), dimension(3, 3) | rmat, | ||
| integer(i4b) | iml0 | ||
| ) |
This is also the matrix that transforms the components of a vector from (c, d, e) coordinates to model coordinates. [Its transpose transforms from model to (c, d, e) coordinates.]
vcc = unit vector for the primary connection, in model coordinates. vcd = unit vector for the first perpendicular direction, in model coordinates. vce = unit vector for the second perpendicular direction, in model coordinates. vcmax = unit vector for the connection with the maximum component perpendicular to the primary connection, in model coordinates. rmat = rotation matrix from model to (c, d, e) coordinates.
Definition at line 283 of file Xt3dAlgorithm.f90.
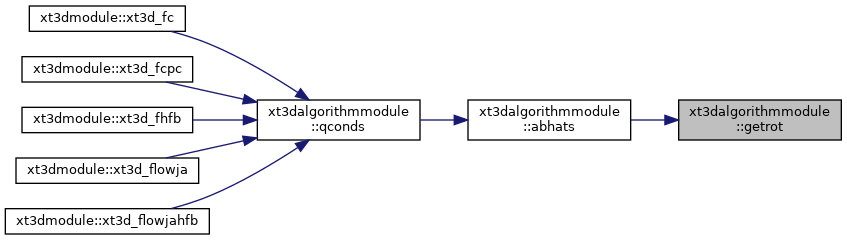
| subroutine xt3dalgorithmmodule::qconds | ( | integer(i4b) | nnbrmx, |
| integer(i4b) | nnbr0, | ||
| integer(i4b), dimension(nnbrmx) | inbr0, | ||
| integer(i4b) | il01, | ||
| real(dp), dimension(nnbrmx, 3) | vc0, | ||
| real(dp), dimension(nnbrmx, 3) | vn0, | ||
| real(dp), dimension(nnbrmx) | dl0, | ||
| real(dp), dimension(nnbrmx) | dl0n, | ||
| real(dp), dimension(3, 3) | ck0, | ||
| integer(i4b) | nnbr1, | ||
| integer(i4b), dimension(nnbrmx) | inbr1, | ||
| integer(i4b) | il10, | ||
| real(dp), dimension(nnbrmx) | vc1, | ||
| real(dp), dimension(nnbrmx) | vn1, | ||
| real(dp), dimension(nnbrmx) | dl1, | ||
| real(dp), dimension(nnbrmx) | dl1n, | ||
| real(dp), dimension(3, 3) | ck1, | ||
| real(dp) | ar01, | ||
| real(dp) | ar10, | ||
| real(dp) | vcthresh, | ||
| logical | allhc0, | ||
| logical | allhc1, | ||
| real(dp) | chat01, | ||
| real(dp), dimension(nnbrmx) | chati0, | ||
| real(dp), dimension(nnbrmx) | chat1j | ||
| ) |
nnbrmx = maximum number of neighbors allowed for a cell. nnbr0 = number of neighbors (local connections) for cell 0. inbr0 = array with the list of neighbors for cell 0. il01 = local node number of cell 1 with respect to cell 0. vc0 = array of connection unit-vectors for cell 0 with its neighbors. vn0 = array of unit normal vectors for cell 0's interfaces. dl0 = array of lengths contributed by cell 0 to its connections with its neighbors. dl0n = array of lengths contributed by cell 0's neighbors to their connections with cell 0. ck0 = conductivity tensor for cell 0. nnbr1 = number of neighbors (local connections) for cell 1. inbr1 = array with the list of neighbors for cell 1. il10 = local node number of cell 0 with respect to cell 1. vc1 = array of connection unit-vectors for cell 1 with its neighbors. vn1 = array of unit normal vectors for cell 1's interfaces. dl1 = array of lengths contributed by cell 1 to its connections with its neighbors. dl1n = array of lengths contributed by cell 1's neighbors to their connections with cell 1. ck1 = conductivity tensor for cell1. ar01 = area of interface (0,1). ar10 = area of interface (1,0). chat01 = "conductance" for connection (0,1). chati0 = array of "conductances" for connections of cell 0. (zero for connection with cell 1, as this connection is already covered by chat01.) chat1j = array of "conductances" for connections of cell 1. (zero for connection with cell 0., as this connection is already covered by chat01.)
Definition at line 47 of file Xt3dAlgorithm.f90.
| subroutine xt3dalgorithmmodule::tranvc | ( | integer(i4b) | nnbrmx, |
| integer(i4b) | nnbrs, | ||
| real(dp), dimension(3, 3) | rmat, | ||
| real(dp), dimension(nnbrmx, 3) | vc, | ||
| real(dp), dimension(nnbrmx, 3) | vccde | ||
| ) |
nnbrs = number of neighbors (local connections) rmat = rotation matrix from (c, d, e) to model coordinates. vc = array of connection unit-vectors with respect to model coordinates. vccde = array of connection unit-vectors with respect to (c, d, e) coordinates.
Definition at line 360 of file Xt3dAlgorithm.f90.