MODFLOW 6  version 6.6.0.dev0
USGS Modular Hydrologic Model
Functions/Subroutines
rcm.f90 File Reference

Go to the source code of this file.

Functions/Subroutines

integer(kind=4) function adj_bandwidth (node_num, adj_num, adj_row, adj)
 
logical function adj_contains_ij (node_num, adj_num, adj_row, adj, i, j)
 
subroutine adj_insert_ij (node_num, adj_max, adj_num, adj_row, adj, i, j)
 
integer(kind=4) function adj_perm_bandwidth (node_num, adj_num, adj_row, adj, perm, perm_inv)
 
subroutine adj_perm_show (node_num, adj_num, adj_row, adj, perm, perm_inv)
 
subroutine adj_print (node_num, adj_num, adj_row, adj, title)
 
subroutine adj_print_some (node_num, node_lo, node_hi, adj_num, adj_row, adj, title)
 
subroutine adj_set (node_num, adj_max, adj_num, adj_row, adj, irow, jcol)
 
subroutine adj_show (node_num, adj_num, adj_row, adj)
 
subroutine degree (root, adj_num, adj_row, adj, mask, deg, iccsze, ls, node_num)
 
subroutine genrcm (node_num, adj_num, adj_row, adj, perm)
 
subroutine graph_01_adj (node_num, adj_num, adj_row, adj)
 
subroutine graph_01_size (node_num, adj_num)
 
subroutine i4_swap (i, j)
 
integer(kind=4) function i4_uniform_ab (a, b, seed)
 
subroutine i4col_compare (m, n, a, i, j, isgn)
 
subroutine i4col_sort_a (m, n, a)
 
subroutine i4col_swap (m, n, a, i, j)
 
subroutine i4mat_print_some (m, n, a, ilo, jlo, ihi, jhi, title)
 
subroutine i4mat_transpose_print (m, n, a, title)
 
subroutine i4mat_transpose_print_some (m, n, a, ilo, jlo, ihi, jhi, title)
 
subroutine i4vec_heap_d (n, a)
 
subroutine i4vec_indicator (n, a)
 
subroutine i4vec_print (n, a, title)
 
subroutine i4vec_reverse (n, a)
 
subroutine i4vec_sort_heap_a (n, a)
 
subroutine level_set (root, adj_num, adj_row, adj, mask, level_num, level_row, level, node_num)
 
subroutine level_set_print (node_num, level_num, level_row, level)
 
subroutine perm_check (n, p, ierror)
 
subroutine perm_inverse3 (n, perm, perm_inv)
 
subroutine perm_uniform (n, seed, p)
 
subroutine r82vec_permute (n, a, p)
 
subroutine r8mat_print_some (m, n, a, ilo, jlo, ihi, jhi, title)
 
subroutine r8mat_transpose_print_some (m, n, a, ilo, jlo, ihi, jhi, title)
 
subroutine rcm (root, adj_num, adj_row, adj, mask, perm, iccsze, node_num)
 
subroutine root_find (root, adj_num, adj_row, adj, mask, level_num, level_row, level, node_num)
 
subroutine sort_heap_external (n, indx, i, j, isgn)
 
subroutine timestamp ()
 
subroutine triangulation_neighbor_triangles (triangle_order, triangle_num, triangle_node, triangle_neighbor)
 
subroutine triangulation_order3_adj_count (node_num, triangle_num, triangle_node, triangle_neighbor, adj_num, adj_col)
 
subroutine triangulation_order3_adj_set (node_num, triangle_num, triangle_node, triangle_neighbor, adj_num, adj_col, adj)
 
subroutine triangulation_order3_example2 (node_num, triangle_num, node_xy, triangle_node, triangle_neighbor)
 
subroutine triangulation_order3_example2_size (node_num, triangle_num, hole_num)
 
subroutine triangulation_order6_adj_count (node_num, triangle_num, triangle_node, triangle_neighbor, adj_num, adj_col)
 
subroutine triangulation_order6_adj_set (node_num, triangle_num, triangle_node, triangle_neighbor, adj_num, adj_col, adj)
 
subroutine triangulation_order6_example2 (node_num, triangle_num, node_xy, triangle_node, triangle_neighbor)
 
subroutine triangulation_order6_example2_size (node_num, triangle_num, hole_num)
 

Function/Subroutine Documentation

◆ adj_bandwidth()

integer ( kind = 4 ) function adj_bandwidth ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj 
)

Definition at line 1 of file rcm.f90.

2 
3  !*****************************************************************************80
4  !
5  !! ADJ_BANDWIDTH computes the bandwidth of an adjacency matrix.
6  !
7  ! Licensing:
8  !
9  ! This code is distributed under the GNU LGPL license.
10  !
11  ! Modified:
12  !
13  ! 11 March 2005
14  !
15  ! Author:
16  !
17  ! John Burkardt
18  !
19  ! Author:
20  !
21  ! Original FORTRAN77 version by Alan George, Joseph Liu.
22  ! FORTRAN90 version by John Burkardt.
23  !
24  ! Reference:
25  !
26  ! Alan George, Joseph Liu,
27  ! Computer Solution of Large Sparse Positive Definite Systems,
28  ! Prentice Hall, 1981.
29  !
30  ! Parameters:
31  !
32  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
33  !
34  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
35  !
36  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
37  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
38  !
39  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
40  ! For each row, it contains the column indices of the nonzero entries.
41  !
42  ! Output, integer ( kind = 4 ) ADJ_BANDWIDTH, the bandwidth of the adjacency
43  ! matrix.
44  !
45  implicit none
46 
47  integer ( kind = 4 ) adj_num
48  integer ( kind = 4 ) node_num
49 
50  integer ( kind = 4 ) adj(adj_num)
51  integer ( kind = 4 ) adj_bandwidth
52  integer ( kind = 4 ) adj_row(node_num+1)
53  integer ( kind = 4 ) band_hi
54  integer ( kind = 4 ) band_lo
55  integer ( kind = 4 ) col
56  integer ( kind = 4 ) i
57  integer ( kind = 4 ) j
58 
59  band_lo = 0
60  band_hi = 0
61 
62  do i = 1, node_num
63 
64  do j = adj_row(i), adj_row(i+1) - 1
65  col = adj(j)
66  band_lo = max( band_lo, i - col )
67  band_hi = max( band_hi, col - i )
68  end do
69 
70  end do
71 
72  adj_bandwidth = band_lo + 1 + band_hi
73 
74  return
adj_bandwidth
integer(kind=4) function adj_bandwidth(node_num, adj_num, adj_row, adj)
Definition: rcm.f90:2

◆ adj_contains_ij()

logical function adj_contains_ij ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 )  i,
integer ( kind = 4 )  j 
)

Definition at line 76 of file rcm.f90.

77 
78  !*****************************************************************************80
79  !
80  !! ADJ_CONTAINS_IJ determines if (I,J) is in an adjacency structure.
81  !
82  ! Licensing:
83  !
84  ! This code is distributed under the GNU LGPL license.
85  !
86  ! Modified:
87  !
88  ! 23 October 2003
89  !
90  ! Author:
91  !
92  ! John Burkardt
93  !
94  ! Parameters:
95  !
96  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
97  !
98  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
99  !
100  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
101  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
102  !
103  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
104  !
105  ! Input, integer ( kind = 4 ) I, J, the two nodes, for which we want to know
106  ! whether I is adjacent to J.
107  !
108  ! Output, logical ADJ_CONTAINS_IJ, is TRUE if I = J, or the adjacency
109  ! structure contains the information that I is adjacent to J.
110  !
111  implicit none
112 
113  integer ( kind = 4 ) adj_num
114  integer ( kind = 4 ) node_num
115 
116  integer ( kind = 4 ) adj(adj_num)
117  logical adj_contains_ij
118  integer ( kind = 4 ) adj_row(node_num+1)
119  integer ( kind = 4 ) i
120  integer ( kind = 4 ) j
121  integer ( kind = 4 ) k
122  integer ( kind = 4 ) khi
123  integer ( kind = 4 ) klo
124  !
125  ! Symmetric entries are not stored.
126  !
127  if ( i == j ) then
128  adj_contains_ij = .true.
129  return
130  end if
131  !
132  ! Illegal I, J entries.
133  !
134  if ( node_num < i ) then
135  adj_contains_ij = .false.
136  return
137  else if ( i < 1 ) then
138  adj_contains_ij = .false.
139  return
140  else if ( node_num < j ) then
141  adj_contains_ij = .false.
142  return
143  else if ( j < 1 ) then
144  adj_contains_ij = .false.
145  return
146  end if
147  !
148  ! Search the adjacency entries already stored for row I,
149  ! to see if J has already been stored.
150  !
151  klo = adj_row(i)
152  khi = adj_row(i+1)-1
153 
154  do k = klo, khi
155 
156  if ( adj(k) == j ) then
157  adj_contains_ij = .true.
158  return
159  end if
160 
161  end do
162 
163  adj_contains_ij = .false.
164 
165  return
adj_contains_ij
logical function adj_contains_ij(node_num, adj_num, adj_row, adj, i, j)
Definition: rcm.f90:77

◆ adj_insert_ij()

subroutine adj_insert_ij ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_max,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_max)  adj,
integer ( kind = 4 )  i,
integer ( kind = 4 )  j 
)

Definition at line 167 of file rcm.f90.

168 
169  !*****************************************************************************80
170  !
171  !! ADJ_INSERT_IJ inserts (I,J) into an adjacency structure.
172  !
173  ! Licensing:
174  !
175  ! This code is distributed under the GNU LGPL license.
176  !
177  ! Modified:
178  !
179  ! 02 January 2007
180  !
181  ! Author:
182  !
183  ! John Burkardt
184  !
185  ! Parameters:
186  !
187  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
188  !
189  ! Input, integer ( kind = 4 ) ADJ_MAX, the maximum number of adjacency
190  ! entries.
191  !
192  ! Input/output, integer ( kind = 4 ) ADJ_NUM, the number of adjacency
193  ! entries.
194  !
195  ! Input/output, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
196  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
197  !
198  ! Input/output, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
199  !
200  ! Input, integer ( kind = 4 ) I, J, the two nodes which are adjacent.
201  !
202  implicit none
203 
204  integer ( kind = 4 ) adj_max
205  integer ( kind = 4 ) node_num
206 
207  integer ( kind = 4 ) adj(adj_max)
208  integer ( kind = 4 ) adj_num
209  integer ( kind = 4 ) adj_row(node_num+1)
210  integer ( kind = 4 ) i
211  integer ( kind = 4 ) j
212  integer ( kind = 4 ) j_spot
213  integer ( kind = 4 ) k
214  !
215  ! A new adjacency entry must be made.
216  ! Check that we're not exceeding the storage allocation for ADJ.
217  !
218  if ( adj_max < adj_num + 1 ) then
219  write ( *, '(a)' ) ' '
220  write ( *, '(a)' ) 'ADJ_INSERT_IJ - Fatal error!'
221  write ( *, '(a)' ) ' All available storage has been used.'
222  write ( *, '(a)' ) ' No more information can be stored!'
223  write ( *, '(a)' ) ' This error occurred for '
224  write ( *, '(a,i8)' ) ' Row I = ', i
225  write ( *, '(a,i8)' ) ' Column J = ', j
226  stop 1
227  end if
228  !
229  ! The action is going to occur between ADJ_ROW(I) and ADJ_ROW(I+1)-1:
230  !
231  j_spot = adj_row(i)
232 
233  do k = adj_row(i), adj_row(i+1) - 1
234 
235  if ( adj(k) == j ) then
236  return
237  else if ( adj(k) < j ) then
238  j_spot = k + 1
239  else
240  exit
241  end if
242 
243  end do
244 
245  adj(j_spot+1:adj_num+1) = adj(j_spot:adj_num)
246  adj(j_spot) = j
247 
248  adj_row(i+1:node_num+1) = adj_row(i+1:node_num+1) + 1
249 
250  adj_num = adj_num + 1
251 
252  return
Here is the caller graph for this function:

◆ adj_perm_bandwidth()

integer ( kind = 4 ) function adj_perm_bandwidth ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  perm,
integer ( kind = 4 ), dimension(node_num)  perm_inv 
)

Definition at line 254 of file rcm.f90.

255 
256  !*****************************************************************************80
257  !
258  !! ADJ_PERM_BANDWIDTH computes the bandwidth of a permuted adjacency matrix.
259  !
260  ! Discussion:
261  !
262  ! The matrix is defined by the adjacency information and a permutation.
263  !
264  ! The routine also computes the bandwidth and the size of the envelope.
265  !
266  ! Licensing:
267  !
268  ! This code is distributed under the GNU LGPL license.
269  !
270  ! Modified:
271  !
272  ! 11 March 2005
273  !
274  ! Author:
275  !
276  ! John Burkardt
277  !
278  ! Reference:
279  !
280  ! Alan George, Joseph Liu,
281  ! Computer Solution of Large Sparse Positive Definite Systems,
282  ! Prentice Hall, 1981.
283  !
284  ! Parameters:
285  !
286  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
287  !
288  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
289  !
290  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
291  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
292  !
293  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
294  ! For each row, it contains the column indices of the nonzero entries.
295  !
296  ! Input, integer ( kind = 4 ) PERM(NODE_NUM), PERM_INV(NODE_NUM), the
297  ! permutation and inverse permutation.
298  !
299  ! Output, integer ( kind = 4 ) ADJ_PERM_BANDWIDTH, the bandwidth of the
300  ! permuted adjacency matrix.
301  !
302  implicit none
303 
304  integer ( kind = 4 ) adj_num
305  integer ( kind = 4 ) node_num
306 
307  integer ( kind = 4 ) adj(adj_num)
308  integer ( kind = 4 ) adj_perm_bandwidth
309  integer ( kind = 4 ) adj_row(node_num+1)
310  integer ( kind = 4 ) band_hi
311  integer ( kind = 4 ) band_lo
312  integer ( kind = 4 ) col
313  integer ( kind = 4 ) i
314  integer ( kind = 4 ) j
315  integer ( kind = 4 ) perm(node_num)
316  integer ( kind = 4 ) perm_inv(node_num)
317 
318  band_lo = 0
319  band_hi = 0
320 
321  do i = 1, node_num
322 
323  do j = adj_row(perm(i)), adj_row(perm(i)+1) - 1
324  col = perm_inv(adj(j))
325  band_lo = max( band_lo, i - col )
326  band_hi = max( band_hi, col - i )
327  end do
328 
329  end do
330 
331  adj_perm_bandwidth = band_lo + 1 + band_hi
332 
333  return
adj_perm_bandwidth
integer(kind=4) function adj_perm_bandwidth(node_num, adj_num, adj_row, adj, perm, perm_inv)
Definition: rcm.f90:255

◆ adj_perm_show()

subroutine adj_perm_show ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  perm,
integer ( kind = 4 ), dimension(node_num)  perm_inv 
)

Definition at line 335 of file rcm.f90.

336 
337  !*****************************************************************************80
338  !
339  !! ADJ_PERM_SHOW displays a symbolic picture of a permuted adjacency matrix.
340  !
341  ! Discussion:
342  !
343  ! The matrix is defined by the adjacency information and a permutation.
344  !
345  ! The routine also computes the bandwidth and the size of the envelope.
346  !
347  ! If no permutation has been done, you must set PERM(I) = PERM_INV(I) = I
348  ! before calling this routine.
349  !
350  ! Licensing:
351  !
352  ! This code is distributed under the GNU LGPL license.
353  !
354  ! Modified:
355  !
356  ! 28 October 2003
357  !
358  ! Author:
359  !
360  ! John Burkardt
361  !
362  ! Reference:
363  !
364  ! Alan George, Joseph Liu,
365  ! Computer Solution of Large Sparse Positive Definite Systems,
366  ! Prentice Hall, 1981.
367  !
368  ! Parameters:
369  !
370  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
371  !
372  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
373  !
374  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
375  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
376  !
377  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
378  ! For each row, it contains the column indices of the nonzero entries.
379  !
380  ! Input, integer ( kind = 4 ) PERM(NODE_NUM), PERM_INV(NODE_NUM), the
381  ! permutation and inverse permutation.
382  !
383  implicit none
384 
385  integer ( kind = 4 ), parameter :: n_max = 100
386 
387  integer ( kind = 4 ) adj_num
388  integer ( kind = 4 ) node_num
389 
390  integer ( kind = 4 ) adj(adj_num)
391  integer ( kind = 4 ) adj_row(node_num+1)
392  character band(n_max)
393  integer ( kind = 4 ) band_lo
394  integer ( kind = 4 ) col
395  integer ( kind = 4 ) i
396  integer ( kind = 4 ) j
397  integer ( kind = 4 ) k
398  integer ( kind = 4 ) nonzero_num
399  integer ( kind = 4 ) perm(node_num)
400  integer ( kind = 4 ) perm_inv(node_num)
401 
402  band_lo = 0
403  nonzero_num = 0
404 
405  if ( n_max < node_num ) then
406  write ( *, '(a)' ) ' '
407  write ( *, '(a)' ) 'ADJ_PERM_SHOW - Fatal error!'
408  write ( *, '(a)' ) ' NODE_NUM is too large!'
409  write ( *, '(a,i8)' ) ' Maximum legal value is ', n_max
410  write ( *, '(a,i8)' ) ' Your input value was ', node_num
411  stop 1
412  end if
413 
414  write ( *, '(a)' ) ' '
415  write ( *, '(a)' ) ' Nonzero structure of matrix:'
416  write ( *, '(a)' ) ' '
417 
418  do i = 1, node_num
419 
420  do k = 1, node_num
421  band(k) = '.'
422  end do
423 
424  band(i) = 'D'
425 
426  do j = adj_row(perm(i)), adj_row(perm(i)+1) - 1
427 
428  col = perm_inv(adj(j))
429 
430  if ( col < i ) then
431  nonzero_num = nonzero_num + 1
432  end if
433 
434  band_lo = max( band_lo, i - col )
435 
436  if ( col /= i ) then
437  band(col) = 'X'
438  end if
439 
440  end do
441 
442  write ( *, '(2x,i8,1x,100a1)' ) i, band(1:node_num)
443 
444  end do
445 
446  write ( *, '(a)' ) ' '
447  write ( *, '(a,i8)' ) ' Lower bandwidth = ', band_lo
448  write ( *, '(a,i8,a)' ) ' Lower envelope contains ', &
449  nonzero_num, ' nonzeros.'
450 
451  return

◆ adj_print()

subroutine adj_print ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
character ( len = * )  title 
)

Definition at line 453 of file rcm.f90.

454 
455  !*****************************************************************************80
456  !
457  !! ADJ_PRINT prints adjacency information.
458  !
459  ! Discussion:
460  !
461  ! The list has the form:
462  !
463  ! Row Nonzeros
464  !
465  ! 1 2 5 9
466  ! 2 7 8 9 15 78 79 81 86 91 99
467  ! 100 103
468  ! 3 48 49 53
469  !
470  ! Licensing:
471  !
472  ! This code is distributed under the GNU LGPL license.
473  !
474  ! Modified:
475  !
476  ! 18 December 2002
477  !
478  ! Author:
479  !
480  ! John Burkardt
481  !
482  ! Parameters:
483  !
484  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
485  !
486  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
487  !
488  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1), organizes the adjacency
489  ! entries into rows. The entries for row I are in entries ADJ_ROW(I)
490  ! through ADJ_ROW(I+1)-1.
491  !
492  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure, which
493  ! contains, for each row, the column indices of the nonzero entries.
494  !
495  ! Input, character ( len = * ) TITLE, a title.
496  !
497  implicit none
498 
499  integer ( kind = 4 ) adj_num
500  integer ( kind = 4 ) node_num
501 
502  integer ( kind = 4 ) adj(adj_num)
503  integer ( kind = 4 ) adj_row(node_num+1)
504  character ( len = * ) title
505 
506  call adj_print_some ( node_num, 1, node_num, adj_num, adj_row, adj, title )
507 
508  return
adj_print_some
subroutine adj_print_some(node_num, node_lo, node_hi, adj_num, adj_row, adj, title)
Definition: rcm.f90:512
Here is the call graph for this function:

◆ adj_print_some()

subroutine adj_print_some ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  node_lo,
integer ( kind = 4 )  node_hi,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
character ( len = * )  title 
)

Definition at line 510 of file rcm.f90.

512 
513  !*****************************************************************************80
514  !
515  !! ADJ_PRINT_SOME prints some adjacency information.
516  !
517  ! Discussion:
518  !
519  ! The list has the form:
520  !
521  ! Row Nonzeros
522  !
523  ! 1 2 5 9
524  ! 2 7 8 9 15 78 79 81 86 91 99
525  ! 100 103
526  ! 3 48 49 53
527  !
528  ! Licensing:
529  !
530  ! This code is distributed under the GNU LGPL license.
531  !
532  ! Modified:
533  !
534  ! 18 December 2002
535  !
536  ! Author:
537  !
538  ! John Burkardt
539  !
540  ! Parameters:
541  !
542  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
543  !
544  ! Input, integer ( kind = 4 ) NODE_LO, NODE_HI, the first and last nodes for
545  ! which the adjacency information is to be printed.
546  !
547  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
548  !
549  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1), organizes the adjacency
550  ! entries into rows. The entries for row I are in entries ADJ_ROW(I)
551  ! through ADJ_ROW(I+1)-1.
552  !
553  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure, which
554  ! contains, for each row, the column indices of the nonzero entries.
555  !
556  ! Input, character ( len = * ) TITLE, a title.
557  !
558  implicit none
559 
560  integer ( kind = 4 ) adj_num
561  integer ( kind = 4 ) node_num
562 
563  integer ( kind = 4 ) adj(adj_num)
564  integer ( kind = 4 ) adj_row(node_num+1)
565  integer ( kind = 4 ) i
566  integer ( kind = 4 ) jhi
567  integer ( kind = 4 ) jlo
568  integer ( kind = 4 ) jmax
569  integer ( kind = 4 ) jmin
570  integer ( kind = 4 ) node_hi
571  integer ( kind = 4 ) node_lo
572  character ( len = * ) title
573 
574  write ( *, '(a)' ) ' '
575  write ( *, '(a)' ) trim( title )
576  write ( *, '(a)' ) ' '
577  write ( *, '(a)' ) ' Sparse adjacency structure:'
578  write ( *, '(a)' ) ' '
579  write ( *, '(a,i8)' ) ' Number of nodes = ', node_num
580  write ( *, '(a,i8)' ) ' Number of adjacencies = ', adj_num
581  write ( *, '(a)' ) ' '
582  write ( *, '(a)' ) ' Node Min Max Nonzeros '
583  write ( *, '(a)' ) ' '
584 
585  do i = node_lo, node_hi
586 
587  jmin = adj_row(i)
588  jmax = adj_row(i+1) - 1
589 
590  if ( jmax < jmin ) then
591 
592  write ( *, '(2x,3i4)' ) i, jmin, jmax
593 
594  else
595 
596  do jlo = jmin, jmax, 5
597 
598  jhi = min( jlo + 4, jmax )
599 
600  if ( jlo == jmin ) then
601  write ( *, '(2x,3i4,3x,5i8)' ) i, jmin, jmax, adj(jlo:jhi)
602  else
603  write ( *, '(2x,12x,3x,5i8)' ) adj(jlo:jhi)
604  end if
605 
606  end do
607 
608  end if
609 
610  end do
611 
612  return
Here is the caller graph for this function:

◆ adj_set()

subroutine adj_set ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_max,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_max)  adj,
integer ( kind = 4 )  irow,
integer ( kind = 4 )  jcol 
)

Definition at line 614 of file rcm.f90.

615 
616  !*****************************************************************************80
617  !
618  !! ADJ_SET sets up the adjacency information.
619  !
620  ! Discussion:
621  !
622  ! The routine records the locations of each nonzero element,
623  ! one at a time.
624  !
625  ! The first call for a given problem should be with IROW or ICOL
626  ! negative. This is a signal indicating the data structure should
627  ! be initialized.
628  !
629  ! Then, for each case in which A(IROW,JCOL) is nonzero, or
630  ! in which IROW is adjacent to JCOL, call this routine once
631  ! to record that fact.
632  !
633  ! Diagonal entries are not to be stored.
634  !
635  ! The matrix is assumed to be symmetric, so setting I adjacent to J
636  ! will also set J adjacent to I.
637  !
638  ! Repeated calls with the same values of IROW and JCOL do not
639  ! actually hurt. No extra storage will be allocated.
640  !
641  ! Licensing:
642  !
643  ! This code is distributed under the GNU LGPL license.
644  !
645  ! Modified:
646  !
647  ! 23 October 2003
648  !
649  ! Author:
650  !
651  ! John Burkardt
652  !
653  ! Parameters:
654  !
655  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
656  !
657  ! Input, integer ( kind = 4 ) ADJ_MAX, the maximum dimension of the
658  ! adjacency array.
659  !
660  ! Input/output, integer ( kind = 4 ) ADJ_NUM, the number of adjaceny entries.
661  !
662  ! Input/output, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
663  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
664  !
665  ! Input/output, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
666  !
667  ! Input, integer ( kind = 4 ) IROW, JCOL, the row and column indices of a
668  ! nonzero entry of the matrix.
669  !
670  implicit none
671 
672  integer ( kind = 4 ) adj_max
673  integer ( kind = 4 ) node_num
674 
675  integer ( kind = 4 ) adj(adj_max)
676  logical adj_contains_ij
677  integer ( kind = 4 ) adj_num
678  integer ( kind = 4 ) adj_row(node_num+1)
679  integer ( kind = 4 ) irow
680  integer ( kind = 4 ) jcol
681  !
682  ! Negative IROW or JCOL indicates the data structure should be initialized.
683  !
684  if ( irow < 0 .or. jcol < 0 ) then
685 
686  write ( *, '(a)' ) ' '
687  write ( *, '(a)' ) 'ADJ_SET - Note:'
688  write ( *, '(a)') ' Initializing adjacency information.'
689  write ( *, '(a,i8)' ) ' Number of nodes NODE_NUM = ', node_num
690  write ( *, '(a,i8)' ) ' Maximum adjacency ADJ_MAX = ', adj_max
691 
692  adj_num = 0
693  adj_row(1:node_num+1) = 1
694  adj(1:adj_max) = 0
695 
696  return
697 
698  end if
699  !
700  ! Diagonal entries are not stored.
701  !
702  if ( irow == jcol ) then
703  return
704  end if
705 
706  if ( node_num < irow ) then
707  write ( *, '(a)' ) ' '
708  write ( *, '(a)' ) 'ADJ_SET - Fatal error!'
709  write ( *, '(a)' ) ' NODE_NUM < IROW.'
710  write ( *, '(a,i8)' ) ' IROW = ', irow
711  write ( *, '(a,i8)' ) ' NODE_NUM = ', node_num
712  stop 1
713  else if ( irow < 1 ) then
714  write ( *, '(a)' ) ' '
715  write ( *, '(a)' ) 'ADJ_SET - Fatal error!'
716  write ( *, '(a)' ) ' IROW < 1.'
717  write ( *, '(a,i8)' ) ' IROW = ', irow
718  stop 1
719  else if ( node_num < jcol ) then
720  write ( *, '(a)' ) ' '
721  write ( *, '(a)' ) 'ADJ_SET - Fatal error!'
722  write ( *, '(a)' ) ' NODE_NUM < JCOL.'
723  write ( *, '(a,i8)' ) ' JCOL = ', jcol
724  write ( *, '(a,i8)' ) ' NODE_NUM = ', node_num
725  stop 1
726  else if ( jcol < 1 ) then
727  write ( *, '(a)' ) ' '
728  write ( *, '(a)' ) 'ADJ_SET - Fatal error!'
729  write ( *, '(a)' ) ' JCOL < 1.'
730  write ( *, '(a,i8)' ) ' JCOL = ', jcol
731  stop 1
732  end if
733 
734  if ( .not. &
735  adj_contains_ij( node_num, adj_num, adj_row, adj, irow, jcol ) ) then
736  call adj_insert_ij ( node_num, adj_max, adj_num, adj_row, adj, irow, jcol )
737  end if
738 
739  if ( .not. &
740  adj_contains_ij( node_num, adj_num, adj_row, adj, jcol, irow ) ) then
741  call adj_insert_ij ( node_num, adj_max, adj_num, adj_row, adj, jcol, irow )
742  end if
743 
744  return
adj_insert_ij
subroutine adj_insert_ij(node_num, adj_max, adj_num, adj_row, adj, i, j)
Definition: rcm.f90:168
Here is the call graph for this function:

◆ adj_show()

subroutine adj_show ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj 
)

Definition at line 746 of file rcm.f90.

747 
748  !*****************************************************************************80
749  !
750  !! ADJ_SHOW displays a symbolic picture of an adjacency matrix.
751  !
752  ! Discussion:
753  !
754  ! The matrix is defined by the adjacency information and a permutation.
755  !
756  ! The routine also computes the bandwidth and the size of the envelope.
757  !
758  ! Licensing:
759  !
760  ! This code is distributed under the GNU LGPL license.
761  !
762  ! Modified:
763  !
764  ! 11 March 2005
765  !
766  ! Author:
767  !
768  ! John Burkardt
769  !
770  ! Reference:
771  !
772  ! Alan George, Joseph Liu,
773  ! Computer Solution of Large Sparse Positive Definite Systems,
774  ! Prentice Hall, 1981.
775  !
776  ! Parameters:
777  !
778  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
779  !
780  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
781  !
782  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
783  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
784  !
785  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
786  ! For each row, it contains the column indices of the nonzero entries.
787  !
788  implicit none
789 
790  integer ( kind = 4 ), parameter :: n_max = 100
791 
792  integer ( kind = 4 ) adj_num
793  integer ( kind = 4 ) node_num
794 
795  integer ( kind = 4 ) adj(adj_num)
796  integer ( kind = 4 ) adj_row(node_num+1)
797  character band(n_max)
798  integer ( kind = 4 ) band_lo
799  integer ( kind = 4 ) col
800  integer ( kind = 4 ) i
801  integer ( kind = 4 ) j
802  integer ( kind = 4 ) k
803  integer ( kind = 4 ) nonzero_num
804 
805  band_lo = 0
806  nonzero_num = 0
807 
808  if ( n_max < node_num ) then
809  write ( *, '(a)' ) ' '
810  write ( *, '(a)' ) 'ADJ_SHOW - Fatal error!'
811  write ( *, '(a)' ) ' NODE_NUM is too large!'
812  write ( *, '(a,i8)' ) ' Maximum legal value is ', n_max
813  write ( *, '(a,i8)' ) ' Your input value was ', node_num
814  stop 1
815  end if
816 
817  write ( *, '(a)' ) ' '
818  write ( *, '(a)' ) ' Nonzero structure of matrix:'
819  write ( *, '(a)' ) ' '
820 
821  do i = 1, node_num
822 
823  do k = 1, node_num
824  band(k) = '.'
825  end do
826 
827  band(i) = 'D'
828 
829  do j = adj_row(i), adj_row(i+1) - 1
830 
831  col = adj(j)
832 
833  if ( col < i ) then
834  nonzero_num = nonzero_num + 1
835  end if
836 
837  band_lo = max( band_lo, i-col )
838  band(col) = 'X'
839 
840  end do
841 
842  write ( *, '(2x,i8,1x,100a1)' ) i, band(1:node_num)
843 
844  end do
845 
846  write ( *, '(a)' ) ' '
847  write ( *, '(a,i8)' ) ' Lower bandwidth = ', band_lo
848  write ( *, '(a,i8,a)' ) ' Lower envelope contains ', &
849  nonzero_num, ' nonzeros.'
850 
851  return

◆ degree()

subroutine degree ( integer ( kind = 4 )  root,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  mask,
integer ( kind = 4 ), dimension(node_num)  deg,
integer ( kind = 4 )  iccsze,
integer ( kind = 4 ), dimension(node_num)  ls,
integer ( kind = 4 )  node_num 
)

Definition at line 853 of file rcm.f90.

855 
856  !*****************************************************************************80
857  !
858  !! DEGREE computes the degrees of the nodes in the connected component.
859  !
860  ! Discussion:
861  !
862  ! The connected component is specified by MASK and ROOT.
863  ! Nodes for which MASK is zero are ignored.
864  !
865  ! Licensing:
866  !
867  ! This code is distributed under the GNU LGPL license.
868  !
869  ! Modified:
870  !
871  ! 05 January 2003
872  !
873  ! Author:
874  !
875  ! Original FORTRAN77 version by Alan George, Joseph Liu.
876  ! FORTRAN90 version by John Burkardt.
877  !
878  ! Reference:
879  !
880  ! Alan George, Joseph Liu,
881  ! Computer Solution of Large Sparse Positive Definite Systems,
882  ! Prentice Hall, 1981.
883  !
884  ! Parameters:
885  !
886  ! Input, integer ( kind = 4 ) ROOT, the node that defines the connected
887  ! component.
888  !
889  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
890  !
891  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
892  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
893  !
894  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
895  ! For each row, it contains the column indices of the nonzero entries.
896  !
897  ! Input, integer ( kind = 4 ) MASK(NODE_NUM), is nonzero for those nodes
898  ! which are to be considered.
899  !
900  ! Output, integer ( kind = 4 ) DEG(NODE_NUM), contains, for each node in
901  ! the connected component, its degree.
902  !
903  ! Output, integer ( kind = 4 ) ICCSIZE, the number of nodes in the
904  ! connected component.
905  !
906  ! Output, integer ( kind = 4 ) LS(NODE_NUM), stores in entries 1 through
907  ! ICCSIZE the nodes in the connected component, starting with ROOT, and
908  ! proceeding by levels.
909  !
910  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
911  !
912  implicit none
913 
914  integer ( kind = 4 ) adj_num
915  integer ( kind = 4 ) node_num
916 
917  integer ( kind = 4 ) adj(adj_num)
918  integer ( kind = 4 ) adj_row(node_num+1)
919  integer ( kind = 4 ) deg(node_num)
920  integer ( kind = 4 ) i
921  integer ( kind = 4 ) iccsze
922  integer ( kind = 4 ) ideg
923  integer ( kind = 4 ) j
924  integer ( kind = 4 ) jstop
925  integer ( kind = 4 ) jstrt
926  integer ( kind = 4 ) lbegin
927  integer ( kind = 4 ) ls(node_num)
928  integer ( kind = 4 ) lvlend
929  integer ( kind = 4 ) lvsize
930  integer ( kind = 4 ) mask(node_num)
931  integer ( kind = 4 ) nbr
932  integer ( kind = 4 ) node
933  integer ( kind = 4 ) root
934  !
935  ! The sign of ADJ_ROW(I) is used to indicate if node I has been considered.
936  !
937  ls(1) = root
938  adj_row(root) = -adj_row(root)
939  lvlend = 0
940  iccsze = 1
941  !
942  ! LBEGIN is the pointer to the beginning of the current level, and
943  ! LVLEND points to the end of this level.
944  !
945  do
946 
947  lbegin = lvlend + 1
948  lvlend = iccsze
949  !
950  ! Find the degrees of nodes in the current level,
951  ! and at the same time, generate the next level.
952  !
953  do i = lbegin, lvlend
954 
955  node = ls(i)
956  jstrt = -adj_row(node)
957  jstop = abs( adj_row(node+1) ) - 1
958  ideg = 0
959 
960  do j = jstrt, jstop
961 
962  nbr = adj(j)
963 
964  if ( mask(nbr) /= 0 ) then
965 
966  ideg = ideg + 1
967 
968  if ( 0 <= adj_row(nbr) ) then
969  adj_row(nbr) = -adj_row(nbr)
970  iccsze = iccsze + 1
971  ls(iccsze) = nbr
972  end if
973 
974  end if
975 
976  end do
977 
978  deg(node) = ideg
979 
980  end do
981  !
982  ! Compute the current level width.
983  !
984  lvsize = iccsze - lvlend
985  !
986  ! If the current level width is nonzero, generate another level.
987  !
988  if ( lvsize == 0 ) then
989  exit
990  end if
991 
992  end do
993  !
994  ! Reset ADJ_ROW to its correct sign and return.
995  !
996  do i = 1, iccsze
997  node = ls(i)
998  adj_row(node) = -adj_row(node)
999  end do
1000 
1001  return
Here is the caller graph for this function:

◆ genrcm()

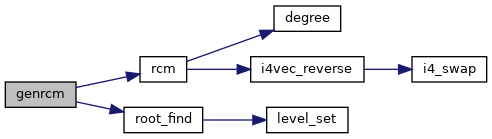
subroutine genrcm ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  perm 
)

Definition at line 1003 of file rcm.f90.

1004 
1005  !*****************************************************************************80
1006  !
1007  !! GENRCM finds the reverse Cuthill-Mckee ordering for a general graph.
1008  !
1009  ! Discussion:
1010  !
1011  ! For each connected component in the graph, the routine obtains
1012  ! an ordering by calling RCM.
1013  !
1014  ! Licensing:
1015  !
1016  ! This code is distributed under the GNU LGPL license.
1017  !
1018  ! Modified:
1019  !
1020  ! 04 January 2003
1021  !
1022  ! Author:
1023  !
1024  ! Original FORTRAN77 version by Alan George, Joseph Liu.
1025  ! FORTRAN90 version by John Burkardt
1026  !
1027  ! Reference:
1028  !
1029  ! Alan George, Joseph Liu,
1030  ! Computer Solution of Large Sparse Positive Definite Systems,
1031  ! Prentice Hall, 1981.
1032  !
1033  ! Parameters:
1034  !
1035  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
1036  !
1037  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
1038  !
1039  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
1040  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
1041  !
1042  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
1043  ! For each row, it contains the column indices of the nonzero entries.
1044  !
1045  ! Output, integer ( kind = 4 ) PERM(NODE_NUM), the RCM ordering.
1046  !
1047  ! Local Parameters:
1048  !
1049  ! Local, integer LEVEL_ROW(NODE_NUM+1), the index vector for a level
1050  ! structure. The level structure is stored in the currently unused
1051  ! spaces in the permutation vector PERM.
1052  !
1053  ! Local, integer MASK(NODE_NUM), marks variables that have been numbered.
1054  !
1055  implicit none
1056 
1057  integer ( kind = 4 ) adj_num
1058  integer ( kind = 4 ) node_num
1059 
1060  integer ( kind = 4 ) adj(adj_num)
1061  integer ( kind = 4 ) adj_row(node_num+1)
1062  integer ( kind = 4 ) i
1063  integer ( kind = 4 ) iccsze
1064  integer ( kind = 4 ) mask(node_num)
1065  integer ( kind = 4 ) level_num
1066  integer ( kind = 4 ) level_row(node_num+1)
1067  integer ( kind = 4 ) num
1068  integer ( kind = 4 ) perm(node_num)
1069  integer ( kind = 4 ) root
1070 
1071  mask(1:node_num) = 1
1072 
1073  num = 1
1074 
1075  do i = 1, node_num
1076  !
1077  ! For each masked connected component...
1078  !
1079  if ( mask(i) /= 0 ) then
1080 
1081  root = i
1082  !
1083  ! Find a pseudo-peripheral node ROOT. The level structure found by
1084  ! ROOT_FIND is stored starting at PERM(NUM).
1085  !
1086  call root_find ( root, adj_num, adj_row, adj, mask, level_num, &
1087  level_row, perm(num), node_num )
1088  !
1089  ! RCM orders the component using ROOT as the starting node.
1090  !
1091  call rcm ( root, adj_num, adj_row, adj, mask, perm(num), iccsze, &
1092  node_num )
1093 
1094  num = num + iccsze
1095  !
1096  ! We can stop once every node is in one of the connected components.
1097  !
1098  if ( node_num < num ) then
1099  return
1100  end if
1101 
1102  end if
1103 
1104  end do
1105 
1106  return
root_find
subroutine root_find(root, adj_num, adj_row, adj, mask, level_num, level_row, level, node_num)
Definition: rcm.f90:3123
rcm
subroutine rcm(root, adj_num, adj_row, adj, mask, perm, iccsze, node_num)
Definition: rcm.f90:2900
Here is the call graph for this function:
Here is the caller graph for this function:

◆ graph_01_adj()

subroutine graph_01_adj ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj 
)

Definition at line 1108 of file rcm.f90.

1109 
1110  !*****************************************************************************80
1111  !
1112  !! GRAPH_01_ADJ returns the adjacency vector for graph 1.
1113  !
1114  ! Licensing:
1115  !
1116  ! This code is distributed under the GNU LGPL license.
1117  !
1118  ! Modified:
1119  !
1120  ! 22 October 2003
1121  !
1122  ! Author:
1123  !
1124  ! John Burkardt
1125  !
1126  ! Reference:
1127  !
1128  ! Alan George, Joseph Liu,
1129  ! Computer Solution of Large Sparse Positive Definite Systems,
1130  ! Prentice Hall, 1981.
1131  !
1132  ! Parameters:
1133  !
1134  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
1135  !
1136  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacencies.
1137  !
1138  ! Output, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1), node pointers into ADJ.
1139  !
1140  ! Output, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency information.
1141  !
1142  implicit none
1143 
1144  integer ( kind = 4 ) adj_num
1145  integer ( kind = 4 ) node_num
1146 
1147  integer ( kind = 4 ) adj(adj_num)
1148  integer ( kind = 4 ) adj_row(node_num+1)
1149 
1150  adj(1:adj_num) = (/ &
1151  4, 6, &
1152  3, 5, 7, 10, &
1153  2, 4, 5, &
1154  1, 3, 6, 9, &
1155  2, 3, 7, &
1156  1, 4, 7, 8, &
1157  2, 5, 6, 8, &
1158  6, 7, &
1159  4, &
1160  2 /)
1161 
1162  adj_row(1:node_num+1) = (/ 1, 3, 7, 10, 14, 17, 21, 25, 27, 28, 29 /)
1163 
1164  return

◆ graph_01_size()

subroutine graph_01_size ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  adj_num 
)

Definition at line 1166 of file rcm.f90.

1167 
1168  !*****************************************************************************80
1169  !
1170  !! GRAPH_01_ADJ_NUM returns the number of adjacencies for graph 1.
1171  !
1172  ! Licensing:
1173  !
1174  ! This code is distributed under the GNU LGPL license.
1175  !
1176  ! Modified:
1177  !
1178  ! 22 October 2003
1179  !
1180  ! Author:
1181  !
1182  ! John Burkardt
1183  !
1184  ! Reference:
1185  !
1186  ! Alan George, Joseph Liu,
1187  ! Computer Solution of Large Sparse Positive Definite Systems,
1188  ! Prentice Hall, 1981.
1189  !
1190  ! Parameters:
1191  !
1192  ! Output, integer ( kind = 4 ) NODE_NUM, the number of items that can
1193  ! be adjacent.
1194  !
1195  ! Output, integer ( kind = 4 ) ADJ_NUM, the number of adjacencies.
1196  !
1197  implicit none
1198 
1199  integer ( kind = 4 ) adj_num
1200  integer ( kind = 4 ) node_num
1201 
1202  node_num = 10
1203  adj_num = 28
1204 
1205  return

◆ i4_swap()

subroutine i4_swap ( integer ( kind = 4 )  i,
integer ( kind = 4 )  j 
)

Definition at line 1207 of file rcm.f90.

1208 
1209  !*****************************************************************************80
1210  !
1211  !! I4_SWAP swaps two I4's.
1212  !
1213  ! Licensing:
1214  !
1215  ! This code is distributed under the GNU LGPL license.
1216  !
1217  ! Modified:
1218  !
1219  ! 30 November 1998
1220  !
1221  ! Author:
1222  !
1223  ! John Burkardt
1224  !
1225  ! Parameters:
1226  !
1227  ! Input/output, integer ( kind = 4 ) I, J. On output, the values of I and
1228  ! J have been interchanged.
1229  !
1230  implicit none
1231 
1232  integer ( kind = 4 ) i
1233  integer ( kind = 4 ) j
1234  integer ( kind = 4 ) k
1235 
1236  k = i
1237  i = j
1238  j = k
1239 
1240  return
Here is the caller graph for this function:

◆ i4_uniform_ab()

integer ( kind = 4 ) function i4_uniform_ab ( integer ( kind = 4 )  a,
integer ( kind = 4 )  b,
integer ( kind = 4 )  seed 
)

Definition at line 1242 of file rcm.f90.

1243 
1244  !*****************************************************************************80
1245  !
1246  !! I4_UNIFORM_AB returns a scaled pseudorandom I4 between A and B.
1247  !
1248  ! Discussion:
1249  !
1250  ! An I4 is an integer ( kind = 4 ) value.
1251  !
1252  ! The pseudorandom number will be scaled to be uniformly distributed
1253  ! between A and B.
1254  !
1255  ! Licensing:
1256  !
1257  ! This code is distributed under the GNU LGPL license.
1258  !
1259  ! Modified:
1260  !
1261  ! 02 October 2012
1262  !
1263  ! Author:
1264  !
1265  ! John Burkardt
1266  !
1267  ! Reference:
1268  !
1269  ! Paul Bratley, Bennett Fox, Linus Schrage,
1270  ! A Guide to Simulation,
1271  ! Second Edition,
1272  ! Springer, 1987,
1273  ! ISBN: 0387964673,
1274  ! LC: QA76.9.C65.B73.
1275  !
1276  ! Bennett Fox,
1277  ! Algorithm 647:
1278  ! Implementation and Relative Efficiency of Quasirandom
1279  ! Sequence Generators,
1280  ! ACM Transactions on Mathematical Software,
1281  ! Volume 12, Number 4, December 1986, pages 362-376.
1282  !
1283  ! Pierre L'Ecuyer,
1284  ! Random Number Generation,
1285  ! in Handbook of Simulation,
1286  ! edited by Jerry Banks,
1287  ! Wiley, 1998,
1288  ! ISBN: 0471134031,
1289  ! LC: T57.62.H37.
1290  !
1291  ! Peter Lewis, Allen Goodman, James Miller,
1292  ! A Pseudo-Random Number Generator for the System/360,
1293  ! IBM Systems Journal,
1294  ! Volume 8, Number 2, 1969, pages 136-143.
1295  !
1296  ! Parameters:
1297  !
1298  ! Input, integer ( kind = 4 ) A, B, the limits of the interval.
1299  !
1300  ! Input/output, integer ( kind = 4 ) SEED, the "seed" value, which
1301  ! should NOT be 0. On output, SEED has been updated.
1302  !
1303  ! Output, integer ( kind = 4 ) I4_UNIFORM_AB, a number between A and B.
1304  !
1305  implicit none
1306 
1307  integer ( kind = 4 ) a
1308  integer ( kind = 4 ) b
1309  integer ( kind = 4 ), parameter :: i4_huge = 2147483647
1310  integer ( kind = 4 ) i4_uniform_ab
1311  integer ( kind = 4 ) k
1312  real ( kind = 4 ) r
1313  integer ( kind = 4 ) seed
1314  integer ( kind = 4 ) value
1315 
1316  if ( seed == 0 ) then
1317  write ( *, '(a)' ) ' '
1318  write ( *, '(a)' ) 'I4_UNIFORM_AB - Fatal error!'
1319  write ( *, '(a)' ) ' Input value of SEED = 0.'
1320  stop 1
1321  end if
1322 
1323  k = seed / 127773
1324 
1325  seed = 16807 * ( seed - k * 127773 ) - k * 2836
1326 
1327  if ( seed < 0 ) then
1328  seed = seed + i4_huge
1329  end if
1330 
1331  r = real( seed, kind = 4 ) * 4.656612875e-10
1332  !
1333  ! Scale R to lie between A-0.5 and B+0.5.
1334  !
1335  r = ( 1.0e+00 - r ) * ( real( min( a, b ), kind = 4 ) - 0.5e+00 ) &
1336  + r * ( real( max( a, b ), kind = 4 ) + 0.5e+00 )
1337  !
1338  ! Use rounding to convert R to an integer between A and B.
1339  !
1340  value = nint( r, kind = 4 )
1341 
1342  value = max( value, min( a, b ) )
1343  value = min( value, max( a, b ) )
1344 
1345  i4_uniform_ab = value
1346 
1347  return
i4_uniform_ab
integer(kind=4) function i4_uniform_ab(a, b, seed)
Definition: rcm.f90:1243

◆ i4col_compare()

subroutine i4col_compare ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(m,n)  a,
integer ( kind = 4 )  i,
integer ( kind = 4 )  j,
integer ( kind = 4 )  isgn 
)

Definition at line 1349 of file rcm.f90.

1350 
1351  !*****************************************************************************80
1352  !
1353  !! I4COL_COMPARE compares columns I and J of an I4COL.
1354  !
1355  ! Example:
1356  !
1357  ! Input:
1358  !
1359  ! M = 3, N = 4, I = 2, J = 4
1360  !
1361  ! A = (
1362  ! 1 2 3 4
1363  ! 5 6 7 8
1364  ! 9 10 11 12 )
1365  !
1366  ! Output:
1367  !
1368  ! ISGN = -1
1369  !
1370  ! Licensing:
1371  !
1372  ! This code is distributed under the GNU LGPL license.
1373  !
1374  ! Modified:
1375  !
1376  ! 30 June 2000
1377  !
1378  ! Author:
1379  !
1380  ! John Burkardt
1381  !
1382  ! Parameters:
1383  !
1384  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns.
1385  !
1386  ! Input, integer ( kind = 4 ) A(M,N), an array of N columns of vectors
1387  ! of length M.
1388  !
1389  ! Input, integer ( kind = 4 ) I, J, the columns to be compared.
1390  ! I and J must be between 1 and N.
1391  !
1392  ! Output, integer ( kind = 4 ) ISGN, the results of the comparison:
1393  ! -1, column I < column J,
1394  ! 0, column I = column J,
1395  ! +1, column J < column I.
1396  !
1397  implicit none
1398 
1399  integer ( kind = 4 ) m
1400  integer ( kind = 4 ) n
1401 
1402  integer ( kind = 4 ) a(m,n)
1403  integer ( kind = 4 ) i
1404  integer ( kind = 4 ) isgn
1405  integer ( kind = 4 ) j
1406  integer ( kind = 4 ) k
1407  !
1408  ! Check.
1409  !
1410  if ( i < 1 .or. n < i ) then
1411  write ( *, '(a)' ) ' '
1412  write ( *, '(a)' ) 'I4COL_COMPARE - Fatal error!'
1413  write ( *, '(a)' ) ' Column index I is out of bounds.'
1414  stop 1
1415  end if
1416 
1417  if ( j < 1 .or. n < j ) then
1418  write ( *, '(a)' ) ' '
1419  write ( *, '(a)' ) 'I4COL_COMPARE - Fatal error!'
1420  write ( *, '(a)' ) ' Column index J is out of bounds.'
1421  stop 1
1422  end if
1423 
1424  isgn = 0
1425 
1426  if ( i == j ) then
1427  return
1428  end if
1429 
1430  k = 1
1431 
1432  do while ( k <= m )
1433 
1434  if ( a(k,i) < a(k,j) ) then
1435  isgn = -1
1436  return
1437  else if ( a(k,j) < a(k,i) ) then
1438  isgn = +1
1439  return
1440  end if
1441 
1442  k = k + 1
1443 
1444  end do
1445 
1446  return
Here is the caller graph for this function:

◆ i4col_sort_a()

subroutine i4col_sort_a ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(m,n)  a 
)

Definition at line 1448 of file rcm.f90.

1449 
1450  !*****************************************************************************80
1451  !
1452  !! I4COL_SORT_A ascending sorts an I4COL.
1453  !
1454  ! Discussion:
1455  !
1456  ! In lexicographic order, the statement "X < Y", applied to two real
1457  ! vectors X and Y of length M, means that there is some index I, with
1458  ! 1 <= I <= M, with the property that
1459  !
1460  ! X(J) = Y(J) for J < I,
1461  ! and
1462  ! X(I) < Y(I).
1463  !
1464  ! In other words, the first time they differ, X is smaller.
1465  !
1466  ! Licensing:
1467  !
1468  ! This code is distributed under the GNU LGPL license.
1469  !
1470  ! Modified:
1471  !
1472  ! 25 September 2001
1473  !
1474  ! Author:
1475  !
1476  ! John Burkardt
1477  !
1478  ! Parameters:
1479  !
1480  ! Input, integer ( kind = 4 ) M, the number of rows of A, and the length of
1481  ! a vector of data.
1482  !
1483  ! Input, integer ( kind = 4 ) N, the number of columns of A.
1484  !
1485  ! Input/output, integer ( kind = 4 ) A(M,N).
1486  ! On input, the array of N columns of M-vectors.
1487  ! On output, the columns of A have been sorted in ascending
1488  ! lexicographic order.
1489  !
1490  implicit none
1491 
1492  integer ( kind = 4 ) m
1493  integer ( kind = 4 ) n
1494 
1495  integer ( kind = 4 ) a(m,n)
1496  integer ( kind = 4 ) i
1497  integer ( kind = 4 ) indx
1498  integer ( kind = 4 ) isgn
1499  integer ( kind = 4 ) j
1500 
1501  if ( m <= 0 ) then
1502  return
1503  end if
1504 
1505  if ( n <= 1 ) then
1506  return
1507  end if
1508  !
1509  ! Initialize.
1510  !
1511  i = 0
1512  indx = 0
1513  isgn = 0
1514  j = 0
1515  !
1516  ! Call the external heap sorter.
1517  !
1518  do
1519 
1520  call sort_heap_external ( n, indx, i, j, isgn )
1521  !
1522  ! Interchange the I and J objects.
1523  !
1524  if ( 0 < indx ) then
1525 
1526  call i4col_swap ( m, n, a, i, j )
1527  !
1528  ! Compare the I and J objects.
1529  !
1530  else if ( indx < 0 ) then
1531 
1532  call i4col_compare ( m, n, a, i, j, isgn )
1533 
1534  else if ( indx == 0 ) then
1535 
1536  exit
1537 
1538  end if
1539 
1540  end do
1541 
1542  return
sort_heap_external
subroutine sort_heap_external(n, indx, i, j, isgn)
Definition: rcm.f90:3318
i4col_compare
subroutine i4col_compare(m, n, a, i, j, isgn)
Definition: rcm.f90:1350
i4col_swap
subroutine i4col_swap(m, n, a, i, j)
Definition: rcm.f90:1545
Here is the call graph for this function:
Here is the caller graph for this function:

◆ i4col_swap()

subroutine i4col_swap ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(m,n)  a,
integer ( kind = 4 )  i,
integer ( kind = 4 )  j 
)

Definition at line 1544 of file rcm.f90.

1545 
1546  !*****************************************************************************80
1547  !
1548  !! I4COL_SWAP swaps columns I and J of an I4COL.
1549  !
1550  ! Example:
1551  !
1552  ! Input:
1553  !
1554  ! M = 3, N = 4, I = 2, J = 4
1555  !
1556  ! A = (
1557  ! 1 2 3 4
1558  ! 5 6 7 8
1559  ! 9 10 11 12 )
1560  !
1561  ! Output:
1562  !
1563  ! A = (
1564  ! 1 4 3 2
1565  ! 5 8 7 6
1566  ! 9 12 11 10 )
1567  !
1568  ! Licensing:
1569  !
1570  ! This code is distributed under the GNU LGPL license.
1571  !
1572  ! Modified:
1573  !
1574  ! 04 April 2001
1575  !
1576  ! Author:
1577  !
1578  ! John Burkardt
1579  !
1580  ! Parameters:
1581  !
1582  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns
1583  ! in the array.
1584  !
1585  ! Input/output, integer ( kind = 4 ) A(M,N), an array of N columns
1586  ! of length M.
1587  !
1588  ! Input, integer ( kind = 4 ) I, J, the columns to be swapped.
1589  !
1590  implicit none
1591 
1592  integer ( kind = 4 ) m
1593  integer ( kind = 4 ) n
1594 
1595  integer ( kind = 4 ) a(m,n)
1596  integer ( kind = 4 ) col(m)
1597  integer ( kind = 4 ) i
1598  integer ( kind = 4 ) j
1599 
1600  if ( i < 1 .or. n < i .or. j < 1 .or. n < j ) then
1601 
1602  write ( *, '(a)' ) ' '
1603  write ( *, '(a)' ) 'I4COL_SWAP - Fatal error!'
1604  write ( *, '(a)' ) ' I or J is out of bounds.'
1605  write ( *, '(a,i8)' ) ' I = ', i
1606  write ( *, '(a,i8)' ) ' J = ', j
1607  write ( *, '(a,i8)' ) ' N = ', n
1608  stop 1
1609 
1610  end if
1611 
1612  if ( i == j ) then
1613  return
1614  end if
1615 
1616  col(1:m) = a(1:m,i)
1617  a(1:m,i) = a(1:m,j)
1618  a(1:m,j) = col(1:m)
1619 
1620  return
Here is the caller graph for this function:

◆ i4mat_print_some()

subroutine i4mat_print_some ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(m,n)  a,
integer ( kind = 4 )  ilo,
integer ( kind = 4 )  jlo,
integer ( kind = 4 )  ihi,
integer ( kind = 4 )  jhi,
character ( len = * )  title 
)

Definition at line 1622 of file rcm.f90.

1623 
1624  !*****************************************************************************80
1625  !
1626  !! I4MAT_PRINT_SOME prints some of an I4MAT.
1627  !
1628  ! Licensing:
1629  !
1630  ! This code is distributed under the GNU LGPL license.
1631  !
1632  ! Modified:
1633  !
1634  ! 04 November 2003
1635  !
1636  ! Author:
1637  !
1638  ! John Burkardt
1639  !
1640  ! Parameters:
1641  !
1642  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns.
1643  !
1644  ! Input, integer ( kind = 4 ) A(M,N), an M by N matrix to be printed.
1645  !
1646  ! Input, integer ( kind = 4 ) ILO, JLO, the first row and column to print.
1647  !
1648  ! Input, integer ( kind = 4 ) IHI, JHI, the last row and column to print.
1649  !
1650  ! Input, character ( len = * ) TITLE, a title.
1651  !
1652  implicit none
1653 
1654  integer ( kind = 4 ), parameter :: incx = 10
1655  integer ( kind = 4 ) m
1656  integer ( kind = 4 ) n
1657 
1658  integer ( kind = 4 ) a(m,n)
1659  character ( len = 7 ) ctemp(incx)
1660  integer ( kind = 4 ) i
1661  integer ( kind = 4 ) i2hi
1662  integer ( kind = 4 ) i2lo
1663  integer ( kind = 4 ) ihi
1664  integer ( kind = 4 ) ilo
1665  integer ( kind = 4 ) inc
1666  integer ( kind = 4 ) j
1667  integer ( kind = 4 ) j2
1668  integer ( kind = 4 ) j2hi
1669  integer ( kind = 4 ) j2lo
1670  integer ( kind = 4 ) jhi
1671  integer ( kind = 4 ) jlo
1672  character ( len = * ) title
1673 
1674  write ( *, '(a)' ) ' '
1675  write ( *, '(a)' ) trim( title )
1676 
1677  do j2lo = max( jlo, 1 ), min( jhi, n ), incx
1678 
1679  j2hi = j2lo + incx - 1
1680  j2hi = min( j2hi, n )
1681  j2hi = min( j2hi, jhi )
1682 
1683  inc = j2hi + 1 - j2lo
1684 
1685  write ( *, '(a)' ) ' '
1686 
1687  do j = j2lo, j2hi
1688  j2 = j + 1 - j2lo
1689  write ( ctemp(j2), '(i7)') j
1690  end do
1691 
1692  write ( *, '('' Col '',10a7)' ) ctemp(1:inc)
1693  write ( *, '(a)' ) ' Row'
1694  write ( *, '(a)' ) ' '
1695 
1696  i2lo = max( ilo, 1 )
1697  i2hi = min( ihi, m )
1698 
1699  do i = i2lo, i2hi
1700 
1701  do j2 = 1, inc
1702 
1703  j = j2lo - 1 + j2
1704 
1705  write ( ctemp(j2), '(i7)' ) a(i,j)
1706 
1707  end do
1708 
1709  write ( *, '(i5,1x,10a7)' ) i, ( ctemp(j), j = 1, inc )
1710 
1711  end do
1712 
1713  end do
1714 
1715  return

◆ i4mat_transpose_print()

subroutine i4mat_transpose_print ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(m,n)  a,
character ( len = * )  title 
)

Definition at line 1717 of file rcm.f90.

1718 
1719  !*****************************************************************************80
1720  !
1721  !! I4MAT_TRANSPOSE_PRINT prints an I4MAT, transposed.
1722  !
1723  ! Licensing:
1724  !
1725  ! This code is distributed under the GNU LGPL license.
1726  !
1727  ! Modified:
1728  !
1729  ! 28 December 2004
1730  !
1731  ! Author:
1732  !
1733  ! John Burkardt
1734  !
1735  ! Parameters:
1736  !
1737  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns.
1738  !
1739  ! Input, integer ( kind = 4 ) A(M,N), an M by N matrix to be printed.
1740  !
1741  ! Input, character ( len = * ) TITLE, a title.
1742  !
1743  implicit none
1744 
1745  integer ( kind = 4 ) m
1746  integer ( kind = 4 ) n
1747 
1748  integer ( kind = 4 ) a(m,n)
1749  character ( len = * ) title
1750 
1751  call i4mat_transpose_print_some ( m, n, a, 1, 1, m, n, title )
1752 
1753  return
i4mat_transpose_print_some
subroutine i4mat_transpose_print_some(m, n, a, ilo, jlo, ihi, jhi, title)
Definition: rcm.f90:1756
Here is the call graph for this function:

◆ i4mat_transpose_print_some()

subroutine i4mat_transpose_print_some ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(m,n)  a,
integer ( kind = 4 )  ilo,
integer ( kind = 4 )  jlo,
integer ( kind = 4 )  ihi,
integer ( kind = 4 )  jhi,
character ( len = * )  title 
)

Definition at line 1755 of file rcm.f90.

1756 
1757  !*****************************************************************************80
1758  !
1759  !! I4MAT_TRANSPOSE_PRINT_SOME prints some of the transpose of an I4MAT.
1760  !
1761  ! Licensing:
1762  !
1763  ! This code is distributed under the GNU LGPL license.
1764  !
1765  ! Modified:
1766  !
1767  ! 09 February 2005
1768  !
1769  ! Author:
1770  !
1771  ! John Burkardt
1772  !
1773  ! Parameters:
1774  !
1775  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns.
1776  !
1777  ! Input, integer ( kind = 4 ) A(M,N), an M by N matrix to be printed.
1778  !
1779  ! Input, integer ( kind = 4 ) ILO, JLO, the first row and column to print.
1780  !
1781  ! Input, integer ( kind = 4 ) IHI, JHI, the last row and column to print.
1782  !
1783  ! Input, character ( len = * ) TITLE, a title.
1784  !
1785  implicit none
1786 
1787  integer ( kind = 4 ), parameter :: incx = 10
1788  integer ( kind = 4 ) m
1789  integer ( kind = 4 ) n
1790 
1791  integer ( kind = 4 ) a(m,n)
1792  character ( len = 7 ) ctemp(incx)
1793  integer ( kind = 4 ) i
1794  integer ( kind = 4 ) i2
1795  integer ( kind = 4 ) i2hi
1796  integer ( kind = 4 ) i2lo
1797  integer ( kind = 4 ) ihi
1798  integer ( kind = 4 ) ilo
1799  integer ( kind = 4 ) inc
1800  integer ( kind = 4 ) j
1801  integer ( kind = 4 ) j2hi
1802  integer ( kind = 4 ) j2lo
1803  integer ( kind = 4 ) jhi
1804  integer ( kind = 4 ) jlo
1805  character ( len = * ) title
1806 
1807  write ( *, '(a)' ) ' '
1808  write ( *, '(a)' ) trim( title )
1809 
1810  do i2lo = max( ilo, 1 ), min( ihi, m ), incx
1811 
1812  i2hi = i2lo + incx - 1
1813  i2hi = min( i2hi, m )
1814  i2hi = min( i2hi, ihi )
1815 
1816  inc = i2hi + 1 - i2lo
1817 
1818  write ( *, '(a)' ) ' '
1819 
1820  do i = i2lo, i2hi
1821  i2 = i + 1 - i2lo
1822  write ( ctemp(i2), '(i7)') i
1823  end do
1824 
1825  write ( *, '('' Row '',10a7)' ) ctemp(1:inc)
1826  write ( *, '(a)' ) ' Col'
1827  write ( *, '(a)' ) ' '
1828 
1829  j2lo = max( jlo, 1 )
1830  j2hi = min( jhi, n )
1831 
1832  do j = j2lo, j2hi
1833 
1834  do i2 = 1, inc
1835 
1836  i = i2lo - 1 + i2
1837 
1838  write ( ctemp(i2), '(i7)' ) a(i,j)
1839 
1840  end do
1841 
1842  write ( *, '(i5,1x,10a7)' ) j, ( ctemp(i), i = 1, inc )
1843 
1844  end do
1845 
1846  end do
1847 
1848  write ( *, '(a)' ) ' '
1849 
1850  return
Here is the caller graph for this function:

◆ i4vec_heap_d()

subroutine i4vec_heap_d ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  a 
)

Definition at line 1852 of file rcm.f90.

1853 
1854  !*****************************************************************************80
1855  !
1856  !! I4VEC_HEAP_D reorders an I4VEC into an descending heap.
1857  !
1858  ! Discussion:
1859  !
1860  ! An I4VEC is a vector of integer values.
1861  !
1862  ! A descending heap is an array A with the property that, for every index J,
1863  ! A(J) >= A(2*J) and A(J) >= A(2*J+1), (as long as the indices
1864  ! 2*J and 2*J+1 are legal).
1865  !
1866  ! A(1)
1867  ! / \
1868  ! A(2) A(3)
1869  ! / \ / \
1870  ! A(4) A(5) A(6) A(7)
1871  ! / \ / \
1872  ! A(8) A(9) A(10) A(11)
1873  !
1874  ! Licensing:
1875  !
1876  ! This code is distributed under the GNU LGPL license.
1877  !
1878  ! Modified:
1879  !
1880  ! 15 April 1999
1881  !
1882  ! Author:
1883  !
1884  ! John Burkardt
1885  !
1886  ! Reference:
1887  !
1888  ! Albert Nijenhuis, Herbert Wilf,
1889  ! Combinatorial Algorithms,
1890  ! Academic Press, 1978, second edition,
1891  ! ISBN 0-12-519260-6.
1892  !
1893  ! Parameters:
1894  !
1895  ! Input, integer ( kind = 4 ) N, the size of the input array.
1896  !
1897  ! Input/output, integer ( kind = 4 ) A(N).
1898  ! On input, an unsorted array.
1899  ! On output, the array has been reordered into a heap.
1900  !
1901  implicit none
1902 
1903  integer ( kind = 4 ) n
1904 
1905  integer ( kind = 4 ) a(n)
1906  integer ( kind = 4 ) i
1907  integer ( kind = 4 ) ifree
1908  integer ( kind = 4 ) key
1909  integer ( kind = 4 ) m
1910  !
1911  ! Only nodes N/2 down to 1 can be "parent" nodes.
1912  !
1913  do i = n/2, 1, -1
1914  !
1915  ! Copy the value out of the parent node.
1916  ! Position IFREE is now "open".
1917  !
1918  key = a(i)
1919  ifree = i
1920 
1921  do
1922  !
1923  ! Positions 2*IFREE and 2*IFREE + 1 are the descendants of position
1924  ! IFREE. (One or both may not exist because they exceed N.)
1925  !
1926  m = 2 * ifree
1927  !
1928  ! Does the first position exist?
1929  !
1930  if ( n < m ) then
1931  exit
1932  end if
1933  !
1934  ! Does the second position exist?
1935  !
1936  if ( m + 1 <= n ) then
1937  !
1938  ! If both positions exist, take the larger of the two values,
1939  ! and update M if necessary.
1940  !
1941  if ( a(m) < a(m+1) ) then
1942  m = m + 1
1943  end if
1944 
1945  end if
1946  !
1947  ! If the large descendant is larger than KEY, move it up,
1948  ! and update IFREE, the location of the free position, and
1949  ! consider the descendants of THIS position.
1950  !
1951  if ( a(m) <= key ) then
1952  exit
1953  end if
1954 
1955  a(ifree) = a(m)
1956  ifree = m
1957 
1958  end do
1959  !
1960  ! Once there is no more shifting to do, KEY moves into the free spot IFREE.
1961  !
1962  a(ifree) = key
1963 
1964  end do
1965 
1966  return
Here is the caller graph for this function:

◆ i4vec_indicator()

subroutine i4vec_indicator ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  a 
)

Definition at line 1968 of file rcm.f90.

1969 
1970  !*****************************************************************************80
1971  !
1972  !! I4VEC_INDICATOR sets an I4VEC to the vector A(I)=I.
1973  !
1974  ! Licensing:
1975  !
1976  ! This code is distributed under the GNU LGPL license.
1977  !
1978  ! Modified:
1979  !
1980  ! 09 November 2000
1981  !
1982  ! Author:
1983  !
1984  ! John Burkardt
1985  !
1986  ! Parameters:
1987  !
1988  ! Input, integer ( kind = 4 ) N, the number of elements of A.
1989  !
1990  ! Output, integer ( kind = 4 ) A(N), the array to be initialized.
1991  !
1992  implicit none
1993 
1994  integer ( kind = 4 ) n
1995 
1996  integer ( kind = 4 ) a(n)
1997  integer ( kind = 4 ) i
1998 
1999  do i = 1, n
2000  a(i) = i
2001  end do
2002 
2003  return
Here is the caller graph for this function:

◆ i4vec_print()

subroutine i4vec_print ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  a,
character ( len = * )  title 
)

Definition at line 2005 of file rcm.f90.

2006 
2007  !*****************************************************************************80
2008  !
2009  !! I4VEC_PRINT prints an I4VEC.
2010  !
2011  ! Licensing:
2012  !
2013  ! This code is distributed under the GNU LGPL license.
2014  !
2015  ! Modified:
2016  !
2017  ! 28 November 2000
2018  !
2019  ! Author:
2020  !
2021  ! John Burkardt
2022  !
2023  ! Parameters:
2024  !
2025  ! Input, integer ( kind = 4 ) N, the number of components of the vector.
2026  !
2027  ! Input, integer ( kind = 4 ) A(N), the vector to be printed.
2028  !
2029  ! Input, character ( len = * ) TITLE, a title to be printed first.
2030  ! TITLE may be blank.
2031  !
2032  implicit none
2033 
2034  integer ( kind = 4 ) n
2035 
2036  integer ( kind = 4 ) a(n)
2037  integer ( kind = 4 ) big
2038  integer ( kind = 4 ) i
2039  character ( len = * ) title
2040 
2041  if ( 0 < len_trim( title ) ) then
2042  write ( *, '(a)' ) ' '
2043  write ( *, '(a)' ) trim( title )
2044  end if
2045 
2046  big = maxval( abs( a(1:n) ) )
2047 
2048  write ( *, '(a)' ) ' '
2049  if ( big < 1000 ) then
2050  do i = 1, n
2051  write ( *, '(2x,i8,2x,i4)' ) i, a(i)
2052  end do
2053  else if ( big < 1000000 ) then
2054  do i = 1, n
2055  write ( *, '(2x,i8,2x,i7)' ) i, a(i)
2056  end do
2057  else
2058  do i = 1, n
2059  write ( *, '(2x,i8,2x,i12)' ) i, a(i)
2060  end do
2061  end if
2062 
2063  return

◆ i4vec_reverse()

subroutine i4vec_reverse ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  a 
)

Definition at line 2065 of file rcm.f90.

2066 
2067  !*****************************************************************************80
2068  !
2069  !! I4VEC_REVERSE reverses the elements of an I4VEC.
2070  !
2071  ! Example:
2072  !
2073  ! Input:
2074  !
2075  ! N = 5,
2076  ! A = ( 11, 12, 13, 14, 15 ).
2077  !
2078  ! Output:
2079  !
2080  ! A = ( 15, 14, 13, 12, 11 ).
2081  !
2082  ! Licensing:
2083  !
2084  ! This code is distributed under the GNU LGPL license.
2085  !
2086  ! Modified:
2087  !
2088  ! 26 July 1999
2089  !
2090  ! Author:
2091  !
2092  ! John Burkardt
2093  !
2094  ! Parameters:
2095  !
2096  ! Input, integer ( kind = 4 ) N, the number of entries in the array.
2097  !
2098  ! Input/output, integer ( kind = 4 ) A(N), the array to be reversed.
2099  !
2100  implicit none
2101 
2102  integer ( kind = 4 ) n
2103 
2104  integer ( kind = 4 ) a(n)
2105  integer ( kind = 4 ) i
2106 
2107  do i = 1, n/2
2108  call i4_swap ( a(i), a(n+1-i) )
2109  end do
2110 
2111  return
i4_swap
subroutine i4_swap(i, j)
Definition: rcm.f90:1208
Here is the call graph for this function:
Here is the caller graph for this function:

◆ i4vec_sort_heap_a()

subroutine i4vec_sort_heap_a ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  a 
)

Definition at line 2113 of file rcm.f90.

2114 
2115  !*****************************************************************************80
2116  !
2117  !! I4VEC_SORT_HEAP_A ascending sorts an I4VEC using heap sort.
2118  !
2119  ! Discussion:
2120  !
2121  ! An I4VEC is a vector of integer values.
2122  !
2123  ! Licensing:
2124  !
2125  ! This code is distributed under the GNU LGPL license.
2126  !
2127  ! Modified:
2128  !
2129  ! 15 April 1999
2130  !
2131  ! Author:
2132  !
2133  ! John Burkardt
2134  !
2135  ! Reference:
2136  !
2137  ! Albert Nijenhuis, Herbert Wilf,
2138  ! Combinatorial Algorithms,
2139  ! Academic Press, 1978, second edition,
2140  ! ISBN 0-12-519260-6.
2141  !
2142  ! Parameters:
2143  !
2144  ! Input, integer ( kind = 4 ) N, the number of entries in the array.
2145  !
2146  ! Input/output, integer ( kind = 4 ) A(N).
2147  ! On input, the array to be sorted;
2148  ! On output, the array has been sorted.
2149  !
2150  implicit none
2151 
2152  integer ( kind = 4 ) n
2153 
2154  integer ( kind = 4 ) a(n)
2155  integer ( kind = 4 ) n1
2156 
2157  if ( n <= 1 ) then
2158  return
2159  end if
2160  !
2161  ! 1: Put A into descending heap form.
2162  !
2163  call i4vec_heap_d ( n, a )
2164  !
2165  ! 2: Sort A.
2166  !
2167  ! The largest object in the heap is in A(1).
2168  ! Move it to position A(N).
2169  !
2170  call i4_swap ( a(1), a(n) )
2171  !
2172  ! Consider the diminished heap of size N1.
2173  !
2174  do n1 = n - 1, 2, -1
2175  !
2176  ! Restore the heap structure of A(1) through A(N1).
2177  !
2178  call i4vec_heap_d ( n1, a )
2179  !
2180  ! Take the largest object from A(1) and move it to A(N1).
2181  !
2182  call i4_swap ( a(1), a(n1) )
2183 
2184  end do
2185 
2186  return
i4vec_heap_d
subroutine i4vec_heap_d(n, a)
Definition: rcm.f90:1853
Here is the call graph for this function:
Here is the caller graph for this function:

◆ level_set()

subroutine level_set ( integer ( kind = 4 )  root,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  mask,
integer ( kind = 4 )  level_num,
integer ( kind = 4 ), dimension(node_num+1)  level_row,
integer ( kind = 4 ), dimension(node_num)  level,
integer ( kind = 4 )  node_num 
)

Definition at line 2188 of file rcm.f90.

2190 
2191  !*****************************************************************************80
2192  !
2193  !! LEVEL_SET generates the connected level structure rooted at a given node.
2194  !
2195  ! Discussion:
2196  !
2197  ! Only nodes for which MASK is nonzero will be considered.
2198  !
2199  ! The root node chosen by the user is assigned level 1, and masked.
2200  ! All (unmasked) nodes reachable from a node in level 1 are
2201  ! assigned level 2 and masked. The process continues until there
2202  ! are no unmasked nodes adjacent to any node in the current level.
2203  ! The number of levels may vary between 2 and NODE_NUM.
2204  !
2205  ! Licensing:
2206  !
2207  ! This code is distributed under the GNU LGPL license.
2208  !
2209  ! Modified:
2210  !
2211  ! 28 October 2003
2212  !
2213  ! Author:
2214  !
2215  ! Original FORTRAN77 version by Alan George, Joseph Liu.
2216  ! FORTRAN90 version by John Burkardt
2217  !
2218  ! Reference:
2219  !
2220  ! Alan George, Joseph Liu,
2221  ! Computer Solution of Large Sparse Positive Definite Systems,
2222  ! Prentice Hall, 1981.
2223  !
2224  ! Parameters:
2225  !
2226  ! Input, integer ( kind = 4 ) ROOT, the node at which the level structure
2227  ! is to be rooted.
2228  !
2229  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
2230  !
2231  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
2232  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
2233  !
2234  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
2235  ! For each row, it contains the column indices of the nonzero entries.
2236  !
2237  ! Input/output, integer ( kind = 4 ) MASK(NODE_NUM). On input, only nodes
2238  ! with nonzero MASK are to be processed. On output, those nodes which were
2239  ! included in the level set have MASK set to 1.
2240  !
2241  ! Output, integer ( kind = 4 ) LEVEL_NUM, the number of levels in the level
2242  ! structure. ROOT is in level 1. The neighbors of ROOT
2243  ! are in level 2, and so on.
2244  !
2245  ! Output, integer ( kind = 4 ) LEVEL_ROW(NODE_NUM+1), LEVEL(NODE_NUM),
2246  ! the rooted level structure.
2247  !
2248  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
2249  !
2250  implicit none
2251 
2252  integer ( kind = 4 ) adj_num
2253  integer ( kind = 4 ) node_num
2254 
2255  integer ( kind = 4 ) adj(adj_num)
2256  integer ( kind = 4 ) adj_row(node_num+1)
2257  integer ( kind = 4 ) i
2258  integer ( kind = 4 ) iccsze
2259  integer ( kind = 4 ) j
2260  integer ( kind = 4 ) jstop
2261  integer ( kind = 4 ) jstrt
2262  integer ( kind = 4 ) lbegin
2263  integer ( kind = 4 ) level_num
2264  integer ( kind = 4 ) level_row(node_num+1)
2265  integer ( kind = 4 ) level(node_num)
2266  integer ( kind = 4 ) lvlend
2267  integer ( kind = 4 ) lvsize
2268  integer ( kind = 4 ) mask(node_num)
2269  integer ( kind = 4 ) nbr
2270  integer ( kind = 4 ) node
2271  integer ( kind = 4 ) root
2272 
2273  mask(root) = 0
2274  level(1) = root
2275  level_num = 0
2276  lvlend = 0
2277  iccsze = 1
2278  !
2279  ! LBEGIN is the pointer to the beginning of the current level, and
2280  ! LVLEND points to the end of this level.
2281  !
2282  do
2283 
2284  lbegin = lvlend + 1
2285  lvlend = iccsze
2286  level_num = level_num + 1
2287  level_row(level_num) = lbegin
2288  !
2289  ! Generate the next level by finding all the masked neighbors of nodes
2290  ! in the current level.
2291  !
2292  do i = lbegin, lvlend
2293 
2294  node = level(i)
2295  jstrt = adj_row(node)
2296  jstop = adj_row(node+1) - 1
2297 
2298  do j = jstrt, jstop
2299 
2300  nbr = adj(j)
2301 
2302  if ( mask(nbr) /= 0 ) then
2303  iccsze = iccsze + 1
2304  level(iccsze) = nbr
2305  mask(nbr) = 0
2306  end if
2307 
2308  end do
2309 
2310  end do
2311  !
2312  ! Compute the current level width (the number of nodes encountered.)
2313  ! If it is positive, generate the next level.
2314  !
2315  lvsize = iccsze - lvlend
2316 
2317  if ( lvsize <= 0 ) then
2318  exit
2319  end if
2320 
2321  end do
2322 
2323  level_row(level_num+1) = lvlend + 1
2324  !
2325  ! Reset MASK to 1 for the nodes in the level structure.
2326  !
2327  mask(level(1:iccsze)) = 1
2328 
2329  return
Here is the caller graph for this function:

◆ level_set_print()

subroutine level_set_print ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  level_num,
integer ( kind = 4 ), dimension(level_num+1)  level_row,
integer ( kind = 4 ), dimension(node_num)  level 
)

Definition at line 2331 of file rcm.f90.

2332 
2333  !*****************************************************************************80
2334  !
2335  !! LEVEL_SET_PRINT prints level set information.
2336  !
2337  ! Licensing:
2338  !
2339  ! This code is distributed under the GNU LGPL license.
2340  !
2341  ! Modified:
2342  !
2343  ! 26 October 2003
2344  !
2345  ! Author:
2346  !
2347  ! John Burkardt
2348  !
2349  ! Parameters:
2350  !
2351  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
2352  !
2353  ! Input, integer ( kind = 4 ) LEVEL_NUM, the number of levels.
2354  !
2355  ! Input, integer ( kind = 4 ) LEVEL_ROW(LEVEL_NUM+1), organizes the entries
2356  ! of LEVEL. The entries for level I are in entries LEVEL_ROW(I)
2357  ! through LEVEL_ROW(I+1)-1.
2358  !
2359  ! Input, integer ( kind = 4 ) LEVEL(NODE_NUM), is simply a list of the
2360  ! nodes in an order induced by the levels.
2361  !
2362  implicit none
2363 
2364  integer ( kind = 4 ) level_num
2365  integer ( kind = 4 ) node_num
2366 
2367  integer ( kind = 4 ) level(node_num)
2368  integer ( kind = 4 ) level_row(level_num+1)
2369  integer ( kind = 4 ) i
2370  integer ( kind = 4 ) jhi
2371  integer ( kind = 4 ) jlo
2372  integer ( kind = 4 ) jmax
2373  integer ( kind = 4 ) jmin
2374 
2375  write ( *, '(a)' ) ' '
2376  write ( *, '(a)' ) 'LEVEL_SET_PRINT'
2377  write ( *, '(a)' ) ' Show the level set structure of a rooted graph.'
2378  write ( *, '(a,i8)' ) ' The number of nodes is ', node_num
2379  write ( *, '(a,i8)' ) ' The number of levels is ', level_num
2380  write ( *, '(a)' ) ' '
2381  write ( *, '(a)' ) ' Level Min Max Nonzeros '
2382  write ( *, '(a)' ) ' '
2383 
2384  do i = 1, level_num
2385 
2386  jmin = level_row(i)
2387  jmax = level_row(i+1) - 1
2388 
2389  if ( jmax < jmin ) then
2390 
2391  write ( *, '(2x,3i4,6x,10i8)' ) i, jmin, jmax
2392 
2393  else
2394 
2395  do jlo = jmin, jmax, 5
2396 
2397  jhi = min( jlo + 4, jmax )
2398 
2399  if ( jlo == jmin ) then
2400  write ( *, '(2x,3i4,3x,5i8)' ) i, jmin, jmax, level(jlo:jhi)
2401  else
2402  write ( *, '(2x,12x,3x,5i8)' ) level(jlo:jhi)
2403  end if
2404 
2405  end do
2406 
2407  end if
2408 
2409  end do
2410 
2411  return

◆ perm_check()

subroutine perm_check ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  p,
integer ( kind = 4 )  ierror 
)

Definition at line 2413 of file rcm.f90.

2414 
2415  !*****************************************************************************80
2416  !
2417  !! PERM_CHECK checks that a vector represents a permutation.
2418  !
2419  ! Discussion:
2420  !
2421  ! The routine verifies that each of the integers from 1
2422  ! to N occurs among the N entries of the permutation.
2423  !
2424  ! Licensing:
2425  !
2426  ! This code is distributed under the GNU LGPL license.
2427  !
2428  ! Modified:
2429  !
2430  ! 01 February 2001
2431  !
2432  ! Author:
2433  !
2434  ! John Burkardt
2435  !
2436  ! Parameters:
2437  !
2438  ! Input, integer ( kind = 4 ) N, the number of entries.
2439  !
2440  ! Input, integer ( kind = 4 ) P(N), the array to check.
2441  !
2442  ! Output, integer ( kind = 4 ) IERROR, error flag.
2443  ! 0, the array represents a permutation.
2444  ! nonzero, the array does not represent a permutation. The smallest
2445  ! missing value is equal to IERROR.
2446  !
2447  implicit none
2448 
2449  integer ( kind = 4 ) n
2450 
2451  integer ( kind = 4 ) ierror
2452  integer ( kind = 4 ) ifind
2453  integer ( kind = 4 ) iseek
2454  integer ( kind = 4 ) p(n)
2455 
2456  ierror = 0
2457 
2458  do iseek = 1, n
2459 
2460  ierror = iseek
2461 
2462  do ifind = 1, n
2463  if ( p(ifind) == iseek ) then
2464  ierror = 0
2465  exit
2466  end if
2467  end do
2468 
2469  if ( ierror /= 0 ) then
2470  return
2471  end if
2472 
2473  end do
2474 
2475  return
Here is the caller graph for this function:

◆ perm_inverse3()

subroutine perm_inverse3 ( integer ( kind = 4 )  n,
integer ( kind = 4 ), dimension(n)  perm,
integer ( kind = 4 ), dimension(n)  perm_inv 
)

Definition at line 2477 of file rcm.f90.

2478 
2479  !*****************************************************************************80
2480  !
2481  !! PERM_INVERSE3 produces the inverse of a given permutation.
2482  !
2483  ! Licensing:
2484  !
2485  ! This code is distributed under the GNU LGPL license.
2486  !
2487  ! Modified:
2488  !
2489  ! 28 October 2003
2490  !
2491  ! Author:
2492  !
2493  ! John Burkardt
2494  !
2495  ! Parameters:
2496  !
2497  ! Input, integer ( kind = 4 ) N, the number of items permuted.
2498  !
2499  ! Input, integer ( kind = 4 ) PERM(N), a permutation.
2500  !
2501  ! Output, integer ( kind = 4 ) PERM_INV(N), the inverse permutation.
2502  !
2503  implicit none
2504 
2505  integer ( kind = 4 ) n
2506 
2507  integer ( kind = 4 ) i
2508  integer ( kind = 4 ) perm(n)
2509  integer ( kind = 4 ) perm_inv(n)
2510 
2511  do i = 1, n
2512  perm_inv(perm(i)) = i
2513  end do
2514 
2515  return

◆ perm_uniform()

subroutine perm_uniform ( integer ( kind = 4 )  n,
integer ( kind = 4 )  seed,
integer ( kind = 4 ), dimension(n)  p 
)

Definition at line 2517 of file rcm.f90.

2518 
2519  !*****************************************************************************80
2520  !
2521  !! PERM_UNIFORM selects a random permutation of N objects.
2522  !
2523  ! Discussion:
2524  !
2525  ! The routine assumes the objects are labeled 1, 2, ... N.
2526  !
2527  ! Licensing:
2528  !
2529  ! This code is distributed under the GNU LGPL license.
2530  !
2531  ! Modified:
2532  !
2533  ! 12 May 2002
2534  !
2535  ! Author:
2536  !
2537  ! Original FORTRAN77 version by Albert Nijenhuis, Herbert Wilf.
2538  ! FORTRAN90 version by John Burkardt
2539  !
2540  ! Reference:
2541  !
2542  ! Albert Nijenhuis, Herbert Wilf,
2543  ! Combinatorial Algorithms,
2544  ! Academic Press, 1978, second edition,
2545  ! ISBN 0-12-519260-6.
2546  !
2547  ! Parameters:
2548  !
2549  ! Input, integer ( kind = 4 ) N, the number of objects to be permuted.
2550  !
2551  ! Input/output, integer ( kind = 4 ) SEED, a seed for the random
2552  ! number generator.
2553  !
2554  ! Output, integer ( kind = 4 ) P(N), a permutation of ( 1, 2, ..., N ),
2555  ! in standard index form.
2556  !
2557  implicit none
2558 
2559  integer ( kind = 4 ) n
2560 
2561  integer ( kind = 4 ) i
2562  integer ( kind = 4 ) i4_uniform_ab
2563  integer ( kind = 4 ) j
2564  integer ( kind = 4 ) p(n)
2565  integer ( kind = 4 ) seed
2566 
2567  call i4vec_indicator ( n, p )
2568 
2569  do i = 1, n
2570  j = i4_uniform_ab( i, n, seed )
2571  call i4_swap ( p(i), p(j) )
2572  end do
2573 
2574  return
i4vec_indicator
subroutine i4vec_indicator(n, a)
Definition: rcm.f90:1969
Here is the call graph for this function:

◆ r82vec_permute()

subroutine r82vec_permute ( integer ( kind = 4 )  n,
real ( kind = 8 ), dimension(ndim,n)  a,
integer ( kind = 4 ), dimension(n)  p 
)

Definition at line 2576 of file rcm.f90.

2577 
2578  !*****************************************************************************80
2579  !
2580  !! R82VEC_PERMUTE permutes an R82VEC in place.
2581  !
2582  ! Discussion:
2583  !
2584  ! This routine permutes an array of real "objects", but the same
2585  ! logic can be used to permute an array of objects of any arithmetic
2586  ! type, or an array of objects of any complexity. The only temporary
2587  ! storage required is enough to store a single object. The number
2588  ! of data movements made is N + the number of cycles of order 2 or more,
2589  ! which is never more than N + N/2.
2590  !
2591  ! Example:
2592  !
2593  ! Input:
2594  !
2595  ! N = 5
2596  ! P = ( 2, 4, 5, 1, 3 )
2597  ! A = ( 1.0, 2.0, 3.0, 4.0, 5.0 )
2598  ! (11.0, 22.0, 33.0, 44.0, 55.0 )
2599  !
2600  ! Output:
2601  !
2602  ! A = ( 2.0, 4.0, 5.0, 1.0, 3.0 )
2603  ! ( 22.0, 44.0, 55.0, 11.0, 33.0 ).
2604  !
2605  ! Licensing:
2606  !
2607  ! This code is distributed under the GNU LGPL license.
2608  !
2609  ! Modified:
2610  !
2611  ! 13 March 2005
2612  !
2613  ! Author:
2614  !
2615  ! John Burkardt
2616  !
2617  ! Parameters:
2618  !
2619  ! Input, integer ( kind = 4 ) N, the number of objects.
2620  !
2621  ! Input/output, real ( kind = 8 ) A(2,N), the array to be permuted.
2622  !
2623  ! Input, integer ( kind = 4 ) P(N), the permutation. P(I) = J means
2624  ! that the I-th element of the output array should be the J-th
2625  ! element of the input array. P must be a legal permutation
2626  ! of the integers from 1 to N, otherwise the algorithm will
2627  ! fail catastrophically.
2628  !
2629  implicit none
2630 
2631  integer ( kind = 4 ) n
2632  integer ( kind = 4 ), parameter :: ndim = 2
2633 
2634  real ( kind = 8 ) a(ndim,n)
2635  real ( kind = 8 ) a_temp(ndim)
2636  integer ( kind = 4 ) ierror
2637  integer ( kind = 4 ) iget
2638  integer ( kind = 4 ) iput
2639  integer ( kind = 4 ) istart
2640  integer ( kind = 4 ) p(n)
2641 
2642  call perm_check ( n, p, ierror )
2643 
2644  if ( ierror /= 0 ) then
2645  write ( *, '(a)' ) ' '
2646  write ( *, '(a)' ) 'R82VEC_PERMUTE - Fatal error!'
2647  write ( *, '(a)' ) ' The input array does not represent'
2648  write ( *, '(a)' ) ' a proper permutation. In particular, the'
2649  write ( *, '(a,i8)' ) ' array is missing the value ', ierror
2650  stop 1
2651  end if
2652  !
2653  ! Search for the next element of the permutation that has not been used.
2654  !
2655  do istart = 1, n
2656 
2657  if ( p(istart) < 0 ) then
2658 
2659  cycle
2660 
2661  else if ( p(istart) == istart ) then
2662 
2663  p(istart) = -p(istart)
2664  cycle
2665 
2666  else
2667 
2668  a_temp(1:ndim) = a(1:ndim,istart)
2669  iget = istart
2670  !
2671  ! Copy the new value into the vacated entry.
2672  !
2673  do
2674 
2675  iput = iget
2676  iget = p(iget)
2677 
2678  p(iput) = -p(iput)
2679 
2680  if ( iget < 1 .or. n < iget ) then
2681  write ( *, '(a)' ) ' '
2682  write ( *, '(a)' ) 'R82VEC_PERMUTE - Fatal error!'
2683  write ( *, '(a)' ) ' A permutation index is out of range.'
2684  write ( *, '(a,i8,a,i8)' ) ' P(', iput, ') = ', iget
2685  stop 1
2686  end if
2687 
2688  if ( iget == istart ) then
2689  a(1:ndim,iput) = a_temp(1:ndim)
2690  exit
2691  end if
2692 
2693  a(1:ndim,iput) = a(1:ndim,iget)
2694 
2695  end do
2696 
2697  end if
2698 
2699  end do
2700  !
2701  ! Restore the signs of the entries.
2702  !
2703  p(1:n) = -p(1:n)
2704 
2705  return
perm_check
subroutine perm_check(n, p, ierror)
Definition: rcm.f90:2414
Here is the call graph for this function:

◆ r8mat_print_some()

subroutine r8mat_print_some ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
real ( kind = 8 ), dimension(m,n)  a,
integer ( kind = 4 )  ilo,
integer ( kind = 4 )  jlo,
integer ( kind = 4 )  ihi,
integer ( kind = 4 )  jhi,
character ( len = * )  title 
)

Definition at line 2707 of file rcm.f90.

2708 
2709  !*****************************************************************************80
2710  !
2711  !! R8MAT_PRINT_SOME prints some of an R8MAT.
2712  !
2713  ! Licensing:
2714  !
2715  ! This code is distributed under the GNU LGPL license.
2716  !
2717  ! Modified:
2718  !
2719  ! 12 September 2004
2720  !
2721  ! Author:
2722  !
2723  ! John Burkardt
2724  !
2725  ! Parameters:
2726  !
2727  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns.
2728  !
2729  ! Input, real ( kind = 8 ) A(M,N), an M by N matrix to be printed.
2730  !
2731  ! Input, integer ( kind = 4 ) ILO, JLO, the first row and column to print.
2732  !
2733  ! Input, integer ( kind = 4 ) IHI, JHI, the last row and column to print.
2734  !
2735  ! Input, character ( len = * ) TITLE, an optional title.
2736  !
2737  implicit none
2738 
2739  integer ( kind = 4 ), parameter :: incx = 5
2740  integer ( kind = 4 ) m
2741  integer ( kind = 4 ) n
2742 
2743  real ( kind = 8 ) a(m,n)
2744  character ( len = 14 ) ctemp(incx)
2745  ! logical d_is_int
2746  integer ( kind = 4 ) i
2747  integer ( kind = 4 ) i2hi
2748  integer ( kind = 4 ) i2lo
2749  integer ( kind = 4 ) ihi
2750  integer ( kind = 4 ) ilo
2751  integer ( kind = 4 ) inc
2752  integer ( kind = 4 ) j
2753  integer ( kind = 4 ) j2
2754  integer ( kind = 4 ) j2hi
2755  integer ( kind = 4 ) j2lo
2756  integer ( kind = 4 ) jhi
2757  integer ( kind = 4 ) jlo
2758  character ( len = * ) title
2759 
2760  if ( 0 < len_trim( title ) ) then
2761  write ( *, '(a)' ) ' '
2762  write ( *, '(a)' ) trim( title )
2763  end if
2764 
2765  do j2lo = max( jlo, 1 ), min( jhi, n ), incx
2766 
2767  j2hi = j2lo + incx - 1
2768  j2hi = min( j2hi, n )
2769  j2hi = min( j2hi, jhi )
2770 
2771  inc = j2hi + 1 - j2lo
2772 
2773  write ( *, '(a)' ) ' '
2774 
2775  do j = j2lo, j2hi
2776  j2 = j + 1 - j2lo
2777  write ( ctemp(j2), '(i7,7x)') j
2778  end do
2779 
2780  write ( *, '('' Col '',5a14)' ) ctemp(1:inc)
2781  write ( *, '(a)' ) ' Row'
2782  write ( *, '(a)' ) ' '
2783 
2784  i2lo = max( ilo, 1 )
2785  i2hi = min( ihi, m )
2786 
2787  do i = i2lo, i2hi
2788 
2789  do j2 = 1, inc
2790 
2791  j = j2lo - 1 + j2
2792 
2793  write ( ctemp(j2), '(g14.6)' ) a(i,j)
2794 
2795  end do
2796 
2797  write ( *, '(i5,1x,5a14)' ) i, ( ctemp(j), j = 1, inc )
2798 
2799  end do
2800 
2801  end do
2802 
2803  return

◆ r8mat_transpose_print_some()

subroutine r8mat_transpose_print_some ( integer ( kind = 4 )  m,
integer ( kind = 4 )  n,
real ( kind = 8 ), dimension(m,n)  a,
integer ( kind = 4 )  ilo,
integer ( kind = 4 )  jlo,
integer ( kind = 4 )  ihi,
integer ( kind = 4 )  jhi,
character ( len = * )  title 
)

Definition at line 2805 of file rcm.f90.

2806 
2807  !*****************************************************************************80
2808  !
2809  !! R8MAT_TRANSPOSE_PRINT_SOME prints some of an R8MAT, transposed.
2810  !
2811  ! Licensing:
2812  !
2813  ! This code is distributed under the GNU LGPL license.
2814  !
2815  ! Modified:
2816  !
2817  ! 14 June 2004
2818  !
2819  ! Author:
2820  !
2821  ! John Burkardt
2822  !
2823  ! Parameters:
2824  !
2825  ! Input, integer ( kind = 4 ) M, N, the number of rows and columns.
2826  !
2827  ! Input, real ( kind = 8 ) A(M,N), an M by N matrix to be printed.
2828  !
2829  ! Input, integer ( kind = 4 ) ILO, JLO, the first row and column to print.
2830  !
2831  ! Input, integer ( kind = 4 ) IHI, JHI, the last row and column to print.
2832  !
2833  ! Input, character ( len = * ) TITLE, an optional title.
2834  !
2835  implicit none
2836 
2837  integer ( kind = 4 ), parameter :: incx = 5
2838  integer ( kind = 4 ) m
2839  integer ( kind = 4 ) n
2840 
2841  real ( kind = 8 ) a(m,n)
2842  character ( len = 14 ) ctemp(incx)
2843  integer ( kind = 4 ) i
2844  integer ( kind = 4 ) i2
2845  integer ( kind = 4 ) i2hi
2846  integer ( kind = 4 ) i2lo
2847  integer ( kind = 4 ) ihi
2848  integer ( kind = 4 ) ilo
2849  integer ( kind = 4 ) inc
2850  integer ( kind = 4 ) j
2851  integer ( kind = 4 ) j2hi
2852  integer ( kind = 4 ) j2lo
2853  integer ( kind = 4 ) jhi
2854  integer ( kind = 4 ) jlo
2855  character ( len = * ) title
2856 
2857  if ( 0 < len_trim( title ) ) then
2858  write ( *, '(a)' ) ' '
2859  write ( *, '(a)' ) trim( title )
2860  end if
2861 
2862  do i2lo = max( ilo, 1 ), min( ihi, m ), incx
2863 
2864  i2hi = i2lo + incx - 1
2865  i2hi = min( i2hi, m )
2866  i2hi = min( i2hi, ihi )
2867 
2868  inc = i2hi + 1 - i2lo
2869 
2870  write ( *, '(a)' ) ' '
2871 
2872  do i = i2lo, i2hi
2873  i2 = i + 1 - i2lo
2874  write ( ctemp(i2), '(i7,7x)') i
2875  end do
2876 
2877  write ( *, '('' Row '',5a14)' ) ctemp(1:inc)
2878  write ( *, '(a)' ) ' Col'
2879  write ( *, '(a)' ) ' '
2880 
2881  j2lo = max( jlo, 1 )
2882  j2hi = min( jhi, n )
2883 
2884  do j = j2lo, j2hi
2885 
2886  do i2 = 1, inc
2887  i = i2lo - 1 + i2
2888  write ( ctemp(i2), '(g14.6)' ) a(i,j)
2889  end do
2890 
2891  write ( *, '(i5,1x,5a14)' ) j, ( ctemp(i), i = 1, inc )
2892 
2893  end do
2894 
2895  end do
2896 
2897  return

◆ rcm()

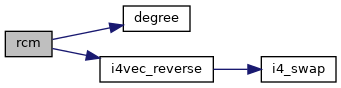
subroutine rcm ( integer ( kind = 4 )  root,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  mask,
integer ( kind = 4 ), dimension(node_num)  perm,
integer ( kind = 4 )  iccsze,
integer ( kind = 4 )  node_num 
)

Definition at line 2899 of file rcm.f90.

2900 
2901  !*****************************************************************************80
2902  !
2903  !! RCM renumbers a connected component by the reverse Cuthill McKee algorithm.
2904  !
2905  ! Discussion:
2906  !
2907  ! The connected component is specified by a node ROOT and a mask.
2908  ! The numbering starts at the root node.
2909  !
2910  ! An outline of the algorithm is as follows:
2911  !
2912  ! X(1) = ROOT.
2913  !
2914  ! for ( I = 1 to N-1 )
2915  ! Find all unlabeled neighbors of X(I),
2916  ! assign them the next available labels, in order of increasing degree.
2917  !
2918  ! When done, reverse the ordering.
2919  !
2920  ! Licensing:
2921  !
2922  ! This code is distributed under the GNU LGPL license.
2923  !
2924  ! Modified:
2925  !
2926  ! 09 August 2013
2927  !
2928  ! Author:
2929  !
2930  ! Original FORTRAN77 version by Alan George, Joseph Liu.
2931  ! FORTRAN90 version by John Burkardt
2932  !
2933  ! Reference:
2934  !
2935  ! Alan George, Joseph Liu,
2936  ! Computer Solution of Large Sparse Positive Definite Systems,
2937  ! Prentice Hall, 1981.
2938  !
2939  ! Parameters:
2940  !
2941  ! Input, integer ( kind = 4 ) ROOT, the node that defines the connected
2942  ! component. It is used as the starting point for the RCM ordering.
2943  ! 1 <= ROOT <= NODE_NUM.
2944  !
2945  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
2946  !
2947  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
2948  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
2949  !
2950  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
2951  ! For each row, it contains the column indices of the nonzero entries.
2952  !
2953  ! Input/output, integer ( kind = 4 ) MASK(NODE_NUM), a mask for the nodes.
2954  ! Only those nodes with nonzero input mask values are considered by the
2955  ! routine. The nodes numbered by RCM will have their mask values
2956  ! set to zero.
2957  !
2958  ! Output, integer ( kind = 4 ) PERM(NODE_NUM), the RCM ordering.
2959  !
2960  ! Output, integer ( kind = 4 ) ICCSZE, the size of the connected component
2961  ! that has been numbered.
2962  !
2963  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
2964  ! 1 <= NODE_NUM.
2965  !
2966  ! Local Parameters:
2967  !
2968  ! Workspace, integer DEG(NODE_NUM), a temporary vector used to hold
2969  ! the degree of the nodes in the section graph specified by mask and root.
2970  !
2971  implicit none
2972 
2973  integer ( kind = 4 ) adj_num
2974  integer ( kind = 4 ) node_num
2975 
2976  integer ( kind = 4 ) adj(adj_num)
2977  integer ( kind = 4 ) adj_row(node_num+1)
2978  integer ( kind = 4 ) deg(node_num)
2979  integer ( kind = 4 ) fnbr
2980  integer ( kind = 4 ) i
2981  integer ( kind = 4 ) iccsze
2982  integer ( kind = 4 ) j
2983  integer ( kind = 4 ) jstop
2984  integer ( kind = 4 ) jstrt
2985  integer ( kind = 4 ) k
2986  integer ( kind = 4 ) l
2987  integer ( kind = 4 ) lbegin
2988  integer ( kind = 4 ) lnbr
2989  integer ( kind = 4 ) lperm
2990  integer ( kind = 4 ) lvlend
2991  integer ( kind = 4 ) mask(node_num)
2992  integer ( kind = 4 ) nbr
2993  integer ( kind = 4 ) node
2994  integer ( kind = 4 ) perm(node_num)
2995  integer ( kind = 4 ) root
2996  !
2997  ! Make sure NODE_NUM is legal.
2998  !
2999  if ( node_num < 1 ) then
3000  write ( *, '(a)' ) ' '
3001  write ( *, '(a)' ) 'RCM - Fatal error!'
3002  write ( *, '(a,i4)' ) ' Illegal input value of NODE_NUM = ', node_num
3003  write ( *, '(a,i4)' ) ' Acceptable values must be positive.'
3004  stop 1
3005  end if
3006  !
3007  ! Make sure ROOT is legal.
3008  !
3009  if ( root < 1 .or. node_num < root ) then
3010  write ( *, '(a)' ) ' '
3011  write ( *, '(a)' ) 'RCM - Fatal error!'
3012  write ( *, '(a,i4)' ) ' Illegal input value of ROOT = ', root
3013  write ( *, '(a,i4)' ) ' Acceptable values are between 1 and ', node_num
3014  stop 1
3015  end if
3016  !
3017  ! Find the degrees of the nodes in the component specified by MASK and ROOT.
3018  !
3019  call degree ( root, adj_num, adj_row, adj, mask, deg, iccsze, perm, node_num )
3020 
3021  mask(root) = 0
3022 
3023  if ( iccsze < 1 ) then
3024  write ( *, '(a)' ) ' '
3025  write ( *, '(a)' ) 'RCM - Fatal error!'
3026  write ( *, '(a,i4)' ) ' Inexplicable component size ICCSZE = ', iccsze
3027  stop 1
3028  end if
3029  !
3030  ! If the connected component is a singleton, there is no reordering to do.
3031  !
3032  if ( iccsze == 1 ) then
3033  return
3034  end if
3035  !
3036  ! Carry out the reordering procedure.
3037  !
3038  ! LBEGIN and LVLEND point to the beginning and
3039  ! the end of the current level respectively.
3040  !
3041  lvlend = 0
3042  lnbr = 1
3043 
3044  do while ( lvlend < lnbr )
3045 
3046  lbegin = lvlend + 1
3047  lvlend = lnbr
3048 
3049  do i = lbegin, lvlend
3050  !
3051  ! For each node in the current level...
3052  !
3053  node = perm(i)
3054  jstrt = adj_row(node)
3055  jstop = adj_row(node+1) - 1
3056  !
3057  ! Find the unnumbered neighbors of NODE.
3058  !
3059  ! FNBR and LNBR point to the first and last neighbors
3060  ! of the current node in PERM.
3061  !
3062  fnbr = lnbr + 1
3063 
3064  do j = jstrt, jstop
3065 
3066  nbr = adj(j)
3067 
3068  if ( mask(nbr) /= 0 ) then
3069  lnbr = lnbr + 1
3070  mask(nbr) = 0
3071  perm(lnbr) = nbr
3072  end if
3073 
3074  end do
3075  !
3076  ! If no neighbors, skip to next node in this level.
3077  !
3078  if ( lnbr <= fnbr ) then
3079  cycle
3080  end if
3081  !
3082  ! Sort the neighbors of NODE in increasing order by degree.
3083  ! Linear insertion is used.
3084  !
3085  k = fnbr
3086 
3087  do while ( k < lnbr )
3088 
3089  l = k
3090  k = k + 1
3091  nbr = perm(k)
3092 
3093  do while ( fnbr < l )
3094 
3095  lperm = perm(l)
3096 
3097  if ( deg(lperm) <= deg(nbr) ) then
3098  exit
3099  end if
3100 
3101  perm(l+1) = lperm
3102  l = l - 1
3103 
3104  end do
3105 
3106  perm(l+1) = nbr
3107 
3108  end do
3109 
3110  end do
3111 
3112  end do
3113  !
3114  ! We now have the Cuthill-McKee ordering.
3115  ! Reverse it to get the Reverse Cuthill-McKee ordering.
3116  !
3117  call i4vec_reverse ( iccsze, perm )
3118 
3119  return
i4vec_reverse
subroutine i4vec_reverse(n, a)
Definition: rcm.f90:2066
degree
subroutine degree(root, adj_num, adj_row, adj, mask, deg, iccsze, ls, node_num)
Definition: rcm.f90:855
Here is the call graph for this function:
Here is the caller graph for this function:

◆ root_find()

subroutine root_find ( integer ( kind = 4 )  root,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_row,
integer ( kind = 4 ), dimension(adj_num)  adj,
integer ( kind = 4 ), dimension(node_num)  mask,
integer ( kind = 4 )  level_num,
integer ( kind = 4 ), dimension(node_num+1)  level_row,
integer ( kind = 4 ), dimension(node_num)  level,
integer ( kind = 4 )  node_num 
)

Definition at line 3121 of file rcm.f90.

3123 
3124  !*****************************************************************************80
3125  !
3126  !! ROOT_FIND finds a pseudo-peripheral node.
3127  !
3128  ! Discussion:
3129  !
3130  ! The diameter of a graph is the maximum distance (number of edges)
3131  ! between any two nodes of the graph.
3132  !
3133  ! The eccentricity of a node is the maximum distance between that
3134  ! node and any other node of the graph.
3135  !
3136  ! A peripheral node is a node whose eccentricity equals the
3137  ! diameter of the graph.
3138  !
3139  ! A pseudo-peripheral node is an approximation to a peripheral node;
3140  ! it may be a peripheral node, but all we know is that we tried our
3141  ! best.
3142  !
3143  ! The routine is given a graph, and seeks pseudo-peripheral nodes,
3144  ! using a modified version of the scheme of Gibbs, Poole and
3145  ! Stockmeyer. It determines such a node for the section subgraph
3146  ! specified by MASK and ROOT.
3147  !
3148  ! The routine also determines the level structure associated with
3149  ! the given pseudo-peripheral node; that is, how far each node
3150  ! is from the pseudo-peripheral node. The level structure is
3151  ! returned as a list of nodes LS, and pointers to the beginning
3152  ! of the list of nodes that are at a distance of 0, 1, 2, ...,
3153  ! NODE_NUM-1 from the pseudo-peripheral node.
3154  !
3155  ! Licensing:
3156  !
3157  ! This code is distributed under the GNU LGPL license.
3158  !
3159  ! Modified:
3160  !
3161  ! 28 October 2003
3162  !
3163  ! Author:
3164  !
3165  ! Original FORTRAN77 version by Alan George, Joseph Liu.
3166  ! FORTRAN90 version by John Burkardt
3167  !
3168  ! Reference:
3169  !
3170  ! Alan George, Joseph Liu,
3171  ! Computer Solution of Large Sparse Positive Definite Systems,
3172  ! Prentice Hall, 1981.
3173  !
3174  ! Norman Gibbs, William Poole, Paul Stockmeyer,
3175  ! An Algorithm for Reducing the Bandwidth and Profile of a Sparse Matrix,
3176  ! SIAM Journal on Numerical Analysis,
3177  ! Volume 13, pages 236-250, 1976.
3178  !
3179  ! Norman Gibbs,
3180  ! Algorithm 509: A Hybrid Profile Reduction Algorithm,
3181  ! ACM Transactions on Mathematical Software,
3182  ! Volume 2, pages 378-387, 1976.
3183  !
3184  ! Parameters:
3185  !
3186  ! Input/output, integer ( kind = 4 ) ROOT. On input, ROOT is a node in the
3187  ! the component of the graph for which a pseudo-peripheral node is
3188  ! sought. On output, ROOT is the pseudo-peripheral node obtained.
3189  !
3190  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacency entries.
3191  !
3192  ! Input, integer ( kind = 4 ) ADJ_ROW(NODE_NUM+1). Information about
3193  ! row I is stored in entries ADJ_ROW(I) through ADJ_ROW(I+1)-1 of ADJ.
3194  !
3195  ! Input, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency structure.
3196  ! For each row, it contains the column indices of the nonzero entries.
3197  !
3198  ! Input, integer ( kind = 4 ) MASK(NODE_NUM), specifies a section subgraph.
3199  ! Nodes for which MASK is zero are ignored by FNROOT.
3200  !
3201  ! Output, integer ( kind = 4 ) LEVEL_NUM, is the number of levels in the
3202  ! level structure rooted at the node ROOT.
3203  !
3204  ! Output, integer ( kind = 4 ) LEVEL_ROW(NODE_NUM+1), LEVEL(NODE_NUM), the
3205  ! level structure array pair containing the level structure found.
3206  !
3207  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
3208  !
3209  implicit none
3210 
3211  integer ( kind = 4 ) adj_num
3212  integer ( kind = 4 ) node_num
3213 
3214  integer ( kind = 4 ) adj(adj_num)
3215  integer ( kind = 4 ) adj_row(node_num+1)
3216  integer ( kind = 4 ) iccsze
3217  integer ( kind = 4 ) j
3218  integer ( kind = 4 ) jstrt
3219  integer ( kind = 4 ) k
3220  integer ( kind = 4 ) kstop
3221  integer ( kind = 4 ) kstrt
3222  integer ( kind = 4 ) level(node_num)
3223  integer ( kind = 4 ) level_num
3224  integer ( kind = 4 ) level_num2
3225  integer ( kind = 4 ) level_row(node_num+1)
3226  integer ( kind = 4 ) mask(node_num)
3227  integer ( kind = 4 ) mindeg
3228  integer ( kind = 4 ) nabor
3229  integer ( kind = 4 ) ndeg
3230  integer ( kind = 4 ) node
3231  integer ( kind = 4 ) root
3232  !
3233  ! Determine the level structure rooted at ROOT.
3234  !
3235  call level_set ( root, adj_num, adj_row, adj, mask, level_num, &
3236  level_row, level, node_num )
3237  !
3238  ! Count the number of nodes in this level structure.
3239  !
3240  iccsze = level_row(level_num+1) - 1
3241  !
3242  ! Extreme case:
3243  ! A complete graph has a level set of only a single level.
3244  ! Every node is equally good (or bad).
3245  !
3246  if ( level_num == 1 ) then
3247  return
3248  end if
3249  !
3250  ! Extreme case:
3251  ! A "line graph" 0--0--0--0--0 has every node in its only level.
3252  ! By chance, we've stumbled on the ideal root.
3253  !
3254  if ( level_num == iccsze ) then
3255  return
3256  end if
3257  !
3258  ! Pick any node from the last level that has minimum degree
3259  ! as the starting point to generate a new level set.
3260  !
3261  do
3262 
3263  mindeg = iccsze
3264 
3265  jstrt = level_row(level_num)
3266  root = level(jstrt)
3267 
3268  if ( jstrt < iccsze ) then
3269 
3270  do j = jstrt, iccsze
3271 
3272  node = level(j)
3273  ndeg = 0
3274  kstrt = adj_row(node)
3275  kstop = adj_row(node+1) - 1
3276 
3277  do k = kstrt, kstop
3278  nabor = adj(k)
3279  if ( 0 < mask(nabor) ) then
3280  ndeg = ndeg + 1
3281  end if
3282  end do
3283 
3284  if ( ndeg < mindeg ) then
3285  root = node
3286  mindeg = ndeg
3287  end if
3288 
3289  end do
3290 
3291  end if
3292  !
3293  ! Generate the rooted level structure associated with this node.
3294  !
3295  call level_set ( root, adj_num, adj_row, adj, mask, level_num2, &
3296  level_row, level, node_num )
3297  !
3298  ! If the number of levels did not increase, accept the new ROOT.
3299  !
3300  if ( level_num2 <= level_num ) then
3301  exit
3302  end if
3303 
3304  level_num = level_num2
3305  !
3306  ! In the unlikely case that ROOT is one endpoint of a line graph,
3307  ! we can exit now.
3308  !
3309  if ( iccsze <= level_num ) then
3310  exit
3311  end if
3312 
3313  end do
3314 
3315  return
level_set
subroutine level_set(root, adj_num, adj_row, adj, mask, level_num, level_row, level, node_num)
Definition: rcm.f90:2190
Here is the call graph for this function:
Here is the caller graph for this function:

◆ sort_heap_external()

subroutine sort_heap_external ( integer ( kind = 4 )  n,
integer ( kind = 4 )  indx,
integer ( kind = 4 )  i,
integer ( kind = 4 )  j,
integer ( kind = 4 )  isgn 
)

Definition at line 3317 of file rcm.f90.

3318 
3319  !*****************************************************************************80
3320  !
3321  !! SORT_HEAP_EXTERNAL externally sorts a list of items into ascending order.
3322  !
3323  ! Discussion:
3324  !
3325  ! The actual list of data is not passed to the routine. Hence this
3326  ! routine may be used to sort integers, reals, numbers, names,
3327  ! dates, shoe sizes, and so on. After each call, the routine asks
3328  ! the user to compare or interchange two items, until a special
3329  ! return value signals that the sorting is completed.
3330  !
3331  ! Licensing:
3332  !
3333  ! This code is distributed under the GNU LGPL license.
3334  !
3335  ! Modified:
3336  !
3337  ! 05 February 2004
3338  !
3339  ! Author:
3340  !
3341  ! Original FORTRAN77 version by Albert Nijenhuis, Herbert Wilf.
3342  ! FORTRAN90 version by John Burkardt
3343  !
3344  ! Reference:
3345  !
3346  ! Albert Nijenhuis, Herbert Wilf,
3347  ! Combinatorial Algorithms,
3348  ! Academic Press, 1978, second edition,
3349  ! ISBN 0-12-519260-6.
3350  !
3351  ! Parameters:
3352  !
3353  ! Input, integer ( kind = 4 ) N, the number of items to be sorted.
3354  !
3355  ! Input/output, integer ( kind = 4 ) INDX, the main communication signal.
3356  !
3357  ! The user must set INDX to 0 before the first call.
3358  ! Thereafter, the user should not change the value of INDX until
3359  ! the sorting is done.
3360  !
3361  ! On return, if INDX is
3362  !
3363  ! greater than 0,
3364  ! * interchange items I and J;
3365  ! * call again.
3366  !
3367  ! less than 0,
3368  ! * compare items I and J;
3369  ! * set ISGN = -1 if I < J, ISGN = +1 if J < I;
3370  ! * call again.
3371  !
3372  ! equal to 0, the sorting is done.
3373  !
3374  ! Output, integer ( kind = 4 ) I, J, the indices of two items.
3375  ! On return with INDX positive, elements I and J should be interchanged.
3376  ! On return with INDX negative, elements I and J should be compared, and
3377  ! the result reported in ISGN on the next call.
3378  !
3379  ! Input, integer ( kind = 4 ) ISGN, results of comparison of elements
3380  ! I and J. (Used only when the previous call returned INDX less than 0).
3381  ! ISGN <= 0 means I is less than or equal to J;
3382  ! 0 <= ISGN means I is greater than or equal to J.
3383  !
3384  implicit none
3385 
3386  integer ( kind = 4 ) i
3387  integer ( kind = 4 ), save :: i_save = 0
3388  integer ( kind = 4 ) indx
3389  integer ( kind = 4 ) isgn
3390  integer ( kind = 4 ) j
3391  integer ( kind = 4 ), save :: j_save = 0
3392  integer ( kind = 4 ), save :: k = 0
3393  integer ( kind = 4 ), save :: k1 = 0
3394  integer ( kind = 4 ) n
3395  integer ( kind = 4 ), save :: n1 = 0
3396  !
3397  ! INDX = 0: This is the first call.
3398  !
3399  if ( indx == 0 ) then
3400 
3401  i_save = 0
3402  j_save = 0
3403  k = n / 2
3404  k1 = k
3405  n1 = n
3406  !
3407  ! INDX < 0: The user is returning the results of a comparison.
3408  !
3409  else if ( indx < 0 ) then
3410 
3411  if ( indx == -2 ) then
3412 
3413  if ( isgn < 0 ) then
3414  i_save = i_save + 1
3415  end if
3416 
3417  j_save = k1
3418  k1 = i_save
3419  indx = -1
3420  i = i_save
3421  j = j_save
3422  return
3423 
3424  end if
3425 
3426  if ( 0 < isgn ) then
3427  indx = 2
3428  i = i_save
3429  j = j_save
3430  return
3431  end if
3432 
3433  if ( k <= 1 ) then
3434 
3435  if ( n1 == 1 ) then
3436  i_save = 0
3437  j_save = 0
3438  indx = 0
3439  else
3440  i_save = n1
3441  n1 = n1 - 1
3442  j_save = 1
3443  indx = 1
3444  end if
3445 
3446  i = i_save
3447  j = j_save
3448  return
3449 
3450  end if
3451 
3452  k = k - 1
3453  k1 = k
3454  !
3455  ! 0 < INDX, the user was asked to make an interchange.
3456  !
3457  else if ( indx == 1 ) then
3458 
3459  k1 = k
3460 
3461  end if
3462 
3463  do
3464 
3465  i_save = 2 * k1
3466 
3467  if ( i_save == n1 ) then
3468  j_save = k1
3469  k1 = i_save
3470  indx = -1
3471  i = i_save
3472  j = j_save
3473  return
3474  else if ( i_save <= n1 ) then
3475  j_save = i_save + 1
3476  indx = -2
3477  i = i_save
3478  j = j_save
3479  return
3480  end if
3481 
3482  if ( k <= 1 ) then
3483  exit
3484  end if
3485 
3486  k = k - 1
3487  k1 = k
3488 
3489  end do
3490 
3491  if ( n1 == 1 ) then
3492  i_save = 0
3493  j_save = 0
3494  indx = 0
3495  i = i_save
3496  j = j_save
3497  else
3498  i_save = n1
3499  n1 = n1 - 1
3500  j_save = 1
3501  indx = 1
3502  i = i_save
3503  j = j_save
3504  end if
3505 
3506  return
Here is the caller graph for this function:

◆ timestamp()

subroutine timestamp

Definition at line 3508 of file rcm.f90.

3509 
3510  !*****************************************************************************80
3511  !
3512  !! TIMESTAMP prints the current YMDHMS date as a time stamp.
3513  !
3514  ! Example:
3515  !
3516  ! 31 May 2001 9:45:54.872 AM
3517  !
3518  ! Licensing:
3519  !
3520  ! This code is distributed under the GNU LGPL license.
3521  !
3522  ! Modified:
3523  !
3524  ! 18 May 2013
3525  !
3526  ! Author:
3527  !
3528  ! John Burkardt
3529  !
3530  ! Parameters:
3531  !
3532  ! None
3533  !
3534  implicit none
3535 
3536  character ( len = 8 ) ampm
3537  integer ( kind = 4 ) d
3538  integer ( kind = 4 ) h
3539  integer ( kind = 4 ) m
3540  integer ( kind = 4 ) mm
3541  character ( len = 9 ), parameter, dimension(12) :: month = (/ &
3542  'January ', 'February ', 'March ', 'April ', &
3543  'May ', 'June ', 'July ', 'August ', &
3544  'September', 'October ', 'November ', 'December ' /)
3545  integer ( kind = 4 ) n
3546  integer ( kind = 4 ) s
3547  integer ( kind = 4 ) values(8)
3548  integer ( kind = 4 ) y
3549 
3550  call date_and_time ( values = values )
3551 
3552  y = values(1)
3553  m = values(2)
3554  d = values(3)
3555  h = values(5)
3556  n = values(6)
3557  s = values(7)
3558  mm = values(8)
3559 
3560  if ( h < 12 ) then
3561  ampm = 'AM'
3562  else if ( h == 12 ) then
3563  if ( n == 0 .and. s == 0 ) then
3564  ampm = 'Noon'
3565  else
3566  ampm = 'PM'
3567  end if
3568  else
3569  h = h - 12
3570  if ( h < 12 ) then
3571  ampm = 'PM'
3572  else if ( h == 12 ) then
3573  if ( n == 0 .and. s == 0 ) then
3574  ampm = 'Midnight'
3575  else
3576  ampm = 'AM'
3577  end if
3578  end if
3579  end if
3580 
3581  write ( *, '(i2,1x,a,1x,i4,2x,i2,a1,i2.2,a1,i2.2,a1,i3.3,1x,a)' ) &
3582  d, trim( month(m) ), y, h, ':', n, ':', s, '.', mm, trim( ampm )
3583 
3584  return

◆ triangulation_neighbor_triangles()

subroutine triangulation_neighbor_triangles ( integer ( kind = 4 )  triangle_order,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor 
)

Definition at line 3587 of file rcm.f90.

3589 
3590  !*****************************************************************************80
3591  !
3592  !! TRIANGULATION_NEIGHBOR_TRIANGLES determines triangle neighbors.
3593  !
3594  ! Discussion:
3595  !
3596  ! A triangulation of a set of nodes can be completely described by
3597  ! the coordinates of the nodes, and the list of nodes that make up
3598  ! each triangle. However, in some cases, it is necessary to know
3599  ! triangle adjacency information, that is, which triangle, if any,
3600  ! is adjacent to a given triangle on a particular side.
3601  !
3602  ! This routine creates a data structure recording this information.
3603  !
3604  ! The primary amount of work occurs in sorting a list of 3 * TRIANGLE_NUM
3605  ! data items.
3606  !
3607  ! Note that ROW is a work array allocated dynamically inside this
3608  ! routine. It is possible, for very large values of TRIANGLE_NUM,
3609  ! that the necessary amount of memory will not be accessible, and the
3610  ! routine will fail. This is a limitation of the implementation of
3611  ! dynamic arrays in FORTRAN90. One way to get around this would be
3612  ! to require the user to declare ROW in the calling routine
3613  ! as an allocatable array, get the necessary memory explicitly with
3614  ! an ALLOCATE statement, and then pass ROW into this routine.
3615  !
3616  ! Of course, the point of dynamic arrays was to make it easy to
3617  ! hide these sorts of temporary work arrays from the poor user!
3618  !
3619  ! This routine was revised to store the edge data in a column
3620  ! array rather than a row array.
3621  !
3622  ! Example:
3623  !
3624  ! The input information from TRIANGLE_NODE:
3625  !
3626  ! Triangle Nodes
3627  ! -------- ---------------
3628  ! 1 3 4 1
3629  ! 2 3 1 2
3630  ! 3 3 2 8
3631  ! 4 2 1 5
3632  ! 5 8 2 13
3633  ! 6 8 13 9
3634  ! 7 3 8 9
3635  ! 8 13 2 5
3636  ! 9 9 13 7
3637  ! 10 7 13 5
3638  ! 11 6 7 5
3639  ! 12 9 7 6
3640  ! 13 10 9 6
3641  ! 14 6 5 12
3642  ! 15 11 6 12
3643  ! 16 10 6 11
3644  !
3645  ! The output information in TRIANGLE_NEIGHBOR:
3646  !
3647  ! Triangle Neighboring Triangles
3648  ! -------- ---------------------
3649  !
3650  ! 1 -1 -1 2
3651  ! 2 1 4 3
3652  ! 3 2 5 7
3653  ! 4 2 -1 8
3654  ! 5 3 8 6
3655  ! 6 5 9 7
3656  ! 7 3 6 -1
3657  ! 8 5 4 10
3658  ! 9 6 10 12
3659  ! 10 9 8 11
3660  ! 11 12 10 14
3661  ! 12 9 11 13
3662  ! 13 -1 12 16
3663  ! 14 11 -1 15
3664  ! 15 16 14 -1
3665  ! 16 13 15 -1
3666  !
3667  ! Licensing:
3668  !
3669  ! This code is distributed under the GNU LGPL license.
3670  !
3671  ! Modified:
3672  !
3673  ! 14 February 2006
3674  !
3675  ! Author:
3676  !
3677  ! John Burkardt
3678  !
3679  ! Parameters:
3680  !
3681  ! Input, integer ( kind = 4 ) TRIANGLE_ORDER, the order of the triangles.
3682  !
3683  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
3684  !
3685  ! Input, integer ( kind = 4 ) TRIANGLE_NODE(TRIANGLE_ORDER,TRIANGLE_NUM),
3686  ! the nodes that make up each triangle.
3687  !
3688  ! Output, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), the three
3689  ! triangles that are direct neighbors of a given triangle.
3690  ! TRIANGLE_NEIGHBOR(1,I) is the index of the triangle which touches side 1,
3691  ! defined by nodes 2 and 3, and so on. TRIANGLE_NEIGHBOR(1,I) is negative
3692  ! if there is no neighbor on that side. In this case, that side of the
3693  ! triangle lies on the boundary of the triangulation.
3694  !
3695  implicit none
3696 
3697  integer ( kind = 4 ) triangle_num
3698  integer ( kind = 4 ) triangle_order
3699 
3700  integer ( kind = 4 ) col(4,3*triangle_num)
3701  integer ( kind = 4 ) i
3702  integer ( kind = 4 ) icol
3703  integer ( kind = 4 ) j
3704  integer ( kind = 4 ) k
3705  integer ( kind = 4 ) side1
3706  integer ( kind = 4 ) side2
3707  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
3708  integer ( kind = 4 ) tri
3709  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
3710  integer ( kind = 4 ) tri1
3711  integer ( kind = 4 ) tri2
3712  !
3713  ! Step 1.
3714  ! From the list of nodes for triangle T, of the form: (I,J,K)
3715  ! construct the three neighbor relations:
3716  !
3717  ! (I,J,3,T) or (J,I,3,T),
3718  ! (J,K,1,T) or (K,J,1,T),
3719  ! (K,I,2,T) or (I,K,2,T)
3720  !
3721  ! where we choose (I,J,1,T) if I < J, or else (J,I,1,T)
3722  !
3723  do tri = 1, triangle_num
3724 
3725  i = triangle_node(1,tri)
3726  j = triangle_node(2,tri)
3727  k = triangle_node(3,tri)
3728 
3729  if ( i < j ) then
3730  col(1:4,3*(tri-1)+1) = (/ i, j, 3, tri /)
3731  else
3732  col(1:4,3*(tri-1)+1) = (/ j, i, 3, tri /)
3733  end if
3734 
3735  if ( j < k ) then
3736  col(1:4,3*(tri-1)+2) = (/ j, k, 1, tri /)
3737  else
3738  col(1:4,3*(tri-1)+2) = (/ k, j, 1, tri /)
3739  end if
3740 
3741  if ( k < i ) then
3742  col(1:4,3*(tri-1)+3) = (/ k, i, 2, tri /)
3743  else
3744  col(1:4,3*(tri-1)+3) = (/ i, k, 2, tri /)
3745  end if
3746 
3747  end do
3748  !
3749  ! Step 2. Perform an ascending dictionary sort on the neighbor relations.
3750  ! We only intend to sort on rows 1 and 2; the routine we call here
3751  ! sorts on rows 1 through 4 but that won't hurt us.
3752  !
3753  ! What we need is to find cases where two triangles share an edge.
3754  ! Say they share an edge defined by the nodes I and J. Then there are
3755  ! two columns of COL that start out ( I, J, ?, ? ). By sorting COL,
3756  ! we make sure that these two columns occur consecutively. That will
3757  ! make it easy to notice that the triangles are neighbors.
3758  !
3759  call i4col_sort_a ( 4, 3*triangle_num, col )
3760  !
3761  ! Step 3. Neighboring triangles show up as consecutive columns with
3762  ! identical first two entries. Whenever you spot this happening,
3763  ! make the appropriate entries in TRIANGLE_NEIGHBOR.
3764  !
3765  triangle_neighbor(1:3,1:triangle_num) = -1
3766 
3767  icol = 1
3768 
3769  do
3770 
3771  if ( 3 * triangle_num <= icol ) then
3772  exit
3773  end if
3774 
3775  if ( col(1,icol) /= col(1,icol+1) .or. col(2,icol) /= col(2,icol+1) ) then
3776  icol = icol + 1
3777  cycle
3778  end if
3779 
3780  side1 = col(3,icol)
3781  tri1 = col(4,icol)
3782  side2 = col(3,icol+1)
3783  tri2 = col(4,icol+1)
3784 
3785  triangle_neighbor(side1,tri1) = tri2
3786  triangle_neighbor(side2,tri2) = tri1
3787 
3788  icol = icol + 2
3789 
3790  end do
3791 
3792  return
i4col_sort_a
subroutine i4col_sort_a(m, n, a)
Definition: rcm.f90:1449
Here is the call graph for this function:

◆ triangulation_order3_adj_count()

subroutine triangulation_order3_adj_count ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_col 
)

Definition at line 3794 of file rcm.f90.

3796 
3797  !*****************************************************************************80
3798  !
3799  !! TRIANGULATION_ORDER3_ADJ_COUNT counts adjacencies in a triangulation.
3800  !
3801  ! Discussion:
3802  !
3803  ! This routine is called to count the adjacencies, so that the
3804  ! appropriate amount of memory can be set aside for storage when
3805  ! the adjacency structure is created.
3806  !
3807  ! The triangulation is assumed to involve 3-node triangles.
3808  !
3809  ! Two nodes are "adjacent" if they are both nodes in some triangle.
3810  ! Also, a node is considered to be adjacent to itself.
3811  !
3812  ! Diagram:
3813  !
3814  ! 3
3815  ! s |\
3816  ! i | \
3817  ! d | \
3818  ! e | \ side 2
3819  ! | \
3820  ! 3 | \
3821  ! | \
3822  ! 1-------2
3823  !
3824  ! side 1
3825  !
3826  ! The local node numbering
3827  !
3828  !
3829  ! 21-22-23-24-25
3830  ! |\ |\ |\ |\ |
3831  ! | \| \| \| \|
3832  ! 16-17-18-19-20
3833  ! |\ |\ |\ |\ |
3834  ! | \| \| \| \|
3835  ! 11-12-13-14-15
3836  ! |\ |\ |\ |\ |
3837  ! | \| \| \| \|
3838  ! 6--7--8--9-10
3839  ! |\ |\ |\ |\ |
3840  ! | \| \| \| \|
3841  ! 1--2--3--4--5
3842  !
3843  ! A sample grid.
3844  !
3845  !
3846  ! Below, we have a chart that summarizes the adjacency relationships
3847  ! in the sample grid. On the left, we list the node, and its neighbors,
3848  ! with an asterisk to indicate the adjacency of the node to itself
3849  ! (in some cases, you want to count this self adjacency and in some
3850  ! you don't). On the right, we list the number of adjacencies to
3851  ! lower-indexed nodes, to the node itself, to higher-indexed nodes,
3852  ! the total number of adjacencies for this node, and the location
3853  ! of the first and last entries required to list this set of adjacencies
3854  ! in a single list of all the adjacencies.
3855  !
3856  ! N Adjacencies Below Self Above Total First Last
3857  !
3858  ! -- -- -- -- -- -- -- -- -- -- -- -- --- 0
3859  ! 1: * 2 6 0 1 2 3 1 3
3860  ! 2: 1 * 3 6 7 1 1 3 5 4 8
3861  ! 3: 2 * 4 7 8 1 1 3 5 9 13
3862  ! 4: 3 * 5 8 9 1 1 3 5 14 18
3863  ! 5: 4 * 9 10 1 1 2 4 19 22
3864  ! 6: 1 2 * 7 11 2 1 2 5 23 27
3865  ! 7: 2 3 6 * 8 11 12 3 1 3 7 28 34
3866  ! 8: 3 4 7 * 9 12 13 3 1 3 7 35 41
3867  ! 9: 4 5 8 * 10 13 14 3 1 3 7 42 48
3868  ! 10: 5 9 * 14 15 2 1 2 5 49 53
3869  ! 11: 6 7 * 12 16 2 1 2 5 54 58
3870  ! 12: 7 8 11 * 13 16 17 3 1 3 7 59 65
3871  ! 13: 8 9 12 * 14 17 18 3 1 3 7 66 72
3872  ! 14: 9 10 13 * 15 18 19 3 1 3 7 73 79
3873  ! 15: 10 14 * 19 20 2 1 2 5 80 84
3874  ! 16: 11 12 * 17 21 2 1 2 5 85 89
3875  ! 17: 12 13 16 * 18 21 22 3 1 3 7 90 96
3876  ! 18: 13 14 17 * 19 22 23 3 1 3 7 97 103
3877  ! 19: 14 15 18 * 20 23 24 3 1 3 7 104 110
3878  ! 20: 15 19 * 24 25 2 1 2 5 111 115
3879  ! 21: 16 17 * 22 2 1 1 4 116 119
3880  ! 22: 17 18 21 * 23 3 1 1 5 120 124
3881  ! 23: 18 19 22 * 24 3 1 1 5 125 129
3882  ! 24: 19 20 23 * 25 3 1 1 5 130 134
3883  ! 25: 20 24 * 2 1 0 3 135 137
3884  ! -- -- -- -- -- -- -- -- -- -- -- -- 138 ---
3885  !
3886  ! Licensing:
3887  !
3888  ! This code is distributed under the GNU LGPL license.
3889  !
3890  ! Modified:
3891  !
3892  ! 24 August 2006
3893  !
3894  ! Author:
3895  !
3896  ! John Burkardt
3897  !
3898  ! Parameters
3899  !
3900  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
3901  !
3902  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
3903  !
3904  ! Input, integer ( kind = 4 ) TRIANGLE_NODE(3,TRIANGLE_NUM), lists the nodes
3905  ! that make up each triangle, in counterclockwise order.
3906  !
3907  ! Input, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), for each
3908  ! side of a triangle, lists the neighboring triangle, or -1 if there is
3909  ! no neighbor.
3910  !
3911  ! Output, integer ( kind = 4 ) ADJ_NUM, the number of adjacencies.
3912  !
3913  ! Output, integer ( kind = 4 ) ADJ_COL(NODE_NUM+1). Information about
3914  ! column J is stored in entries ADJ_COL(J) through ADJ_COL(J+1)-1 of ADJ.
3915  !
3916  implicit none
3917 
3918  integer ( kind = 4 ) node_num
3919  integer ( kind = 4 ) triangle_num
3920  integer ( kind = 4 ), parameter :: triangle_order = 3
3921 
3922  integer ( kind = 4 ) adj_num
3923  integer ( kind = 4 ) adj_col(node_num+1)
3924  integer ( kind = 4 ) i
3925  integer ( kind = 4 ) n1
3926  integer ( kind = 4 ) n2
3927  integer ( kind = 4 ) n3
3928  integer ( kind = 4 ) triangle
3929  integer ( kind = 4 ) triangle2
3930  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
3931  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
3932 
3933  adj_num = 0
3934  !
3935  ! Set every node to be adjacent to itself.
3936  !
3937  adj_col(1:node_num) = 1
3938  !
3939  ! Examine each triangle.
3940  !
3941  do triangle = 1, triangle_num
3942 
3943  n1 = triangle_node(1,triangle)
3944  n2 = triangle_node(2,triangle)
3945  n3 = triangle_node(3,triangle)
3946  !
3947  ! Add edge (1,2) if this is the first occurrence,
3948  ! that is, if the edge (1,2) is on a boundary (TRIANGLE2 <= 0)
3949  ! or if this triangle is the first of the pair in which the edge
3950  ! occurs (TRIANGLE < TRIANGLE2).
3951  !
3952  triangle2 = triangle_neighbor(1,triangle)
3953 
3954  if ( triangle2 < 0 .or. triangle < triangle2 ) then
3955  adj_col(n1) = adj_col(n1) + 1
3956  adj_col(n2) = adj_col(n2) + 1
3957  end if
3958  !
3959  ! Add edge (2,3).
3960  !
3961  triangle2 = triangle_neighbor(2,triangle)
3962 
3963  if ( triangle2 < 0 .or. triangle < triangle2 ) then
3964  adj_col(n2) = adj_col(n2) + 1
3965  adj_col(n3) = adj_col(n3) + 1
3966  end if
3967  !
3968  ! Add edge (3,1).
3969  !
3970  triangle2 = triangle_neighbor(3,triangle)
3971 
3972  if ( triangle2 < 0 .or. triangle < triangle2 ) then
3973  adj_col(n1) = adj_col(n1) + 1
3974  adj_col(n3) = adj_col(n3) + 1
3975  end if
3976 
3977  end do
3978  !
3979  ! We used ADJ_COL to count the number of entries in each column.
3980  ! Convert it to pointers into the ADJ array.
3981  !
3982  adj_col(2:node_num+1) = adj_col(1:node_num)
3983 
3984  adj_col(1) = 1
3985  do i = 2, node_num + 1
3986  adj_col(i) = adj_col(i-1) + adj_col(i)
3987  end do
3988 
3989  adj_num = adj_col(node_num+1) - 1
3990 
3991  return

◆ triangulation_order3_adj_set()

subroutine triangulation_order3_adj_set ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_col,
integer ( kind = 4 ), dimension(adj_num)  adj 
)

Definition at line 3993 of file rcm.f90.

3995 
3996  !*****************************************************************************80
3997  !
3998  !! TRIANGULATION_ORDER3_ADJ_SET sets adjacencies in a triangulation.
3999  !
4000  ! Discussion:
4001  !
4002  ! This routine is called to count the adjacencies, so that the
4003  ! appropriate amount of memory can be set aside for storage when
4004  ! the adjacency structure is created.
4005  !
4006  ! The triangulation is assumed to involve 3-node triangles.
4007  !
4008  ! Two nodes are "adjacent" if they are both nodes in some triangle.
4009  ! Also, a node is considered to be adjacent to itself.
4010  !
4011  ! This routine can be used to create the compressed column storage
4012  ! for a linear triangle finite element discretization of
4013  ! Poisson's equation in two dimensions.
4014  !
4015  ! Diagram:
4016  !
4017  ! 3
4018  ! s |\
4019  ! i | \
4020  ! d | \
4021  ! e | \ side 2
4022  ! | \
4023  ! 3 | \
4024  ! | \
4025  ! 1-------2
4026  !
4027  ! side 1
4028  !
4029  ! The local node numbering
4030  !
4031  !
4032  ! 21-22-23-24-25
4033  ! |\ |\ |\ |\ |
4034  ! | \| \| \| \|
4035  ! 16-17-18-19-20
4036  ! |\ |\ |\ |\ |
4037  ! | \| \| \| \|
4038  ! 11-12-13-14-15
4039  ! |\ |\ |\ |\ |
4040  ! | \| \| \| \|
4041  ! 6--7--8--9-10
4042  ! |\ |\ |\ |\ |
4043  ! | \| \| \| \|
4044  ! 1--2--3--4--5
4045  !
4046  ! A sample grid
4047  !
4048  !
4049  ! Below, we have a chart that summarizes the adjacency relationships
4050  ! in the sample grid. On the left, we list the node, and its neighbors,
4051  ! with an asterisk to indicate the adjacency of the node to itself
4052  ! (in some cases, you want to count this self adjacency and in some
4053  ! you don't). On the right, we list the number of adjacencies to
4054  ! lower-indexed nodes, to the node itself, to higher-indexed nodes,
4055  ! the total number of adjacencies for this node, and the location
4056  ! of the first and last entries required to list this set of adjacencies
4057  ! in a single list of all the adjacencies.
4058  !
4059  ! N Adjacencies Below Self Above Total First Last
4060  !
4061  ! -- -- -- -- -- -- -- -- -- -- -- -- --- 0
4062  ! 1: * 2 6 0 1 2 3 1 3
4063  ! 2: 1 * 3 6 7 1 1 3 5 4 8
4064  ! 3: 2 * 4 7 8 1 1 3 5 9 13
4065  ! 4: 3 * 5 8 9 1 1 3 5 14 18
4066  ! 5: 4 * 9 10 1 1 2 4 19 22
4067  ! 6: 1 2 * 7 11 2 1 2 5 23 27
4068  ! 7: 2 3 6 * 8 11 12 3 1 3 7 28 34
4069  ! 8: 3 4 7 * 9 12 13 3 1 3 7 35 41
4070  ! 9: 4 5 8 * 10 13 14 3 1 3 7 42 48
4071  ! 10: 5 9 * 14 15 2 1 2 5 49 53
4072  ! 11: 6 7 * 12 16 2 1 2 5 54 58
4073  ! 12: 7 8 11 * 13 16 17 3 1 3 7 59 65
4074  ! 13: 8 9 12 * 14 17 18 3 1 3 7 66 72
4075  ! 14: 9 10 13 * 15 18 19 3 1 3 7 73 79
4076  ! 15: 10 14 * 19 20 2 1 2 5 80 84
4077  ! 16: 11 12 * 17 21 2 1 2 5 85 89
4078  ! 17: 12 13 16 * 18 21 22 3 1 3 7 90 96
4079  ! 18: 13 14 17 * 19 22 23 3 1 3 7 97 103
4080  ! 19: 14 15 18 * 20 23 24 3 1 3 7 104 110
4081  ! 20: 15 19 * 24 25 2 1 2 5 111 115
4082  ! 21: 16 17 * 22 2 1 1 4 116 119
4083  ! 22: 17 18 21 * 23 3 1 1 5 120 124
4084  ! 23: 18 19 22 * 24 3 1 1 5 125 129
4085  ! 24: 19 20 23 * 25 3 1 1 5 130 134
4086  ! 25: 20 24 * 2 1 0 3 135 137
4087  ! -- -- -- -- -- -- -- -- -- -- -- -- 138 ---
4088  !
4089  ! Licensing:
4090  !
4091  ! This code is distributed under the GNU LGPL license.
4092  !
4093  ! Modified:
4094  !
4095  ! 24 August 2006
4096  !
4097  ! Author:
4098  !
4099  ! John Burkardt
4100  !
4101  ! Parameters
4102  !
4103  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
4104  !
4105  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
4106  !
4107  ! Input, integer ( kind = 4 ) TRIANGLE_NODE(3,TRIANGLE_NUM), lists the nodes
4108  ! that make up each triangle in counterclockwise order.
4109  !
4110  ! Input, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), for each
4111  ! side of a triangle, lists the neighboring triangle, or -1 if there is
4112  ! no neighbor.
4113  !
4114  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacencies.
4115  !
4116  ! Input, integer ( kind = 4 ) ADJ_COL(NODE_NUM+1). Information about
4117  ! column J is stored in entries ADJ_COL(J) through ADJ_COL(J+1)-1 of ADJ.
4118  !
4119  ! Output, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency information.
4120  !
4121  implicit none
4122 
4123  integer ( kind = 4 ) adj_num
4124  integer ( kind = 4 ) node_num
4125  integer ( kind = 4 ) triangle_num
4126  integer ( kind = 4 ), parameter :: triangle_order = 3
4127 
4128  integer ( kind = 4 ) adj(adj_num)
4129  integer ( kind = 4 ) adj_copy(node_num)
4130  integer ( kind = 4 ) adj_col(node_num+1)
4131  integer ( kind = 4 ) k1
4132  integer ( kind = 4 ) k2
4133  integer ( kind = 4 ) n1
4134  integer ( kind = 4 ) n2
4135  integer ( kind = 4 ) n3
4136  integer ( kind = 4 ) node
4137  integer ( kind = 4 ) triangle
4138  integer ( kind = 4 ) triangle2
4139  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
4140  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
4141 
4142  adj(1:adj_num) = -1
4143  adj_copy(1:node_num) = adj_col(1:node_num)
4144  !
4145  ! Set every node to be adjacent to itself.
4146  !
4147  do node = 1, node_num
4148  adj(adj_copy(node)) = node
4149  adj_copy(node) = adj_copy(node) + 1
4150  end do
4151  !
4152  ! Examine each triangle.
4153  !
4154  do triangle = 1, triangle_num
4155 
4156  n1 = triangle_node(1,triangle)
4157  n2 = triangle_node(2,triangle)
4158  n3 = triangle_node(3,triangle)
4159  !
4160  ! Add edge (1,2) if this is the first occurrence,
4161  ! that is, if the edge (1,2) is on a boundary (TRIANGLE2 <= 0)
4162  ! or if this triangle is the first of the pair in which the edge
4163  ! occurs (TRIANGLE < TRIANGLE2).
4164  !
4165  triangle2 = triangle_neighbor(1,triangle)
4166 
4167  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4168  adj(adj_copy(n1)) = n2
4169  adj_copy(n1) = adj_copy(n1) + 1
4170  adj(adj_copy(n2)) = n1
4171  adj_copy(n2) = adj_copy(n2) + 1
4172  end if
4173  !
4174  ! Add edge (2,3).
4175  !
4176  triangle2 = triangle_neighbor(2,triangle)
4177 
4178  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4179  adj(adj_copy(n2)) = n3
4180  adj_copy(n2) = adj_copy(n2) + 1
4181  adj(adj_copy(n3)) = n2
4182  adj_copy(n3) = adj_copy(n3) + 1
4183  end if
4184  !
4185  ! Add edge (3,1).
4186  !
4187  triangle2 = triangle_neighbor(3,triangle)
4188 
4189  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4190  adj(adj_copy(n1)) = n3
4191  adj_copy(n1) = adj_copy(n1) + 1
4192  adj(adj_copy(n3)) = n1
4193  adj_copy(n3) = adj_copy(n3) + 1
4194  end if
4195 
4196  end do
4197  !
4198  ! Ascending sort the entries for each node.
4199  !
4200  do node = 1, node_num
4201  k1 = adj_col(node)
4202  k2 = adj_col(node+1) - 1
4203  call i4vec_sort_heap_a ( k2+1-k1, adj(k1:k2) )
4204  end do
4205 
4206  return
i4vec_sort_heap_a
subroutine i4vec_sort_heap_a(n, a)
Definition: rcm.f90:2114
Here is the call graph for this function:

◆ triangulation_order3_example2()

subroutine triangulation_order3_example2 ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
real ( kind = 8 ), dimension(dim_num,node_num)  node_xy,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor 
)

Definition at line 4208 of file rcm.f90.

4210 
4211  !*****************************************************************************80
4212  !
4213  !! TRIANGULATION_ORDER3_EXAMPLE2 returns an example triangulation.
4214  !
4215  ! Discussion:
4216  !
4217  ! This triangulation is actually a Delaunay triangulation.
4218  !
4219  ! The appropriate input values of NODE_NUM and TRIANGLE_NUM can be
4220  ! determined by calling TRIANGULATION_ORDER3_EXAMPLE2_SIZE first.
4221  !
4222  ! Diagram:
4223  !
4224  ! 21-22-23-24-25
4225  ! |\ |\ |\ |\ |
4226  ! | \| \| \| \|
4227  ! 16-17-18-19-20
4228  ! |\ |\ |\ |\ |
4229  ! | \| \| \| \|
4230  ! 11-12-13-14-15
4231  ! |\ |\ |\ |\ |
4232  ! | \| \| \| \|
4233  ! 6--7--8--9-10
4234  ! |\ |\ |\ |\ |
4235  ! | \| \| \| \|
4236  ! 1--2--3--4--5
4237  !
4238  ! Licensing:
4239  !
4240  ! This code is distributed under the GNU LGPL license.
4241  !
4242  ! Modified:
4243  !
4244  ! 03 January 2007
4245  !
4246  ! Author:
4247  !
4248  ! John Burkardt
4249  !
4250  ! Parameters
4251  !
4252  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
4253  !
4254  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
4255  !
4256  ! Output, real ( kind = 8 ) NODE_XY(2,NODE_NUM), the coordinates of the
4257  ! nodes.
4258  !
4259  ! Output, integer ( kind = 4 ) TRIANGLE_NODE(3,TRIANGLE_NUM), lists the
4260  ! nodes that make up each triangle, in counterclockwise order.
4261  !
4262  ! Output, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), for each
4263  ! side of a triangle, lists the neighboring triangle, or -1 if there is
4264  ! no neighbor.
4265  !
4266  implicit none
4267 
4268  integer ( kind = 4 ), parameter :: dim_num = 2
4269  integer ( kind = 4 ) node_num
4270  integer ( kind = 4 ) triangle_num
4271  integer ( kind = 4 ), parameter :: triangle_order = 3
4272 
4273  real ( kind = 8 ) node_xy(dim_num,node_num)
4274  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
4275  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
4276 
4277  node_xy = reshape( (/ &
4278  0.0d+00, 0.0d+00, &
4279  1.0d+00, 0.0d+00, &
4280  2.0d+00, 0.0d+00, &
4281  3.0d+00, 0.0d+00, &
4282  4.0d+00, 0.0d+00, &
4283  0.0d+00, 1.0d+00, &
4284  1.0d+00, 1.0d+00, &
4285  2.0d+00, 1.0d+00, &
4286  3.0d+00, 1.0d+00, &
4287  4.0d+00, 1.0d+00, &
4288  0.0d+00, 2.0d+00, &
4289  1.0d+00, 2.0d+00, &
4290  2.0d+00, 2.0d+00, &
4291  3.0d+00, 2.0d+00, &
4292  4.0d+00, 2.0d+00, &
4293  0.0d+00, 3.0d+00, &
4294  1.0d+00, 3.0d+00, &
4295  2.0d+00, 3.0d+00, &
4296  3.0d+00, 3.0d+00, &
4297  4.0d+00, 3.0d+00, &
4298  0.0d+00, 4.0d+00, &
4299  1.0d+00, 4.0d+00, &
4300  2.0d+00, 4.0d+00, &
4301  3.0d+00, 4.0d+00, &
4302  4.0d+00, 4.0d+00 &
4303  /), (/ dim_num, node_num /) )
4304 
4305  triangle_node(1:triangle_order,1:triangle_num) = reshape( (/ &
4306  1, 2, 6, &
4307  7, 6, 2, &
4308  2, 3, 7, &
4309  8, 7, 3, &
4310  3, 4, 8, &
4311  9, 8, 4, &
4312  4, 5, 9, &
4313  10, 9, 5, &
4314  6, 7, 11, &
4315  12, 11, 7, &
4316  7, 8, 12, &
4317  13, 12, 8, &
4318  8, 9, 13, &
4319  14, 13, 9, &
4320  9, 10, 14, &
4321  15, 14, 10, &
4322  11, 12, 16, &
4323  17, 16, 12, &
4324  12, 13, 17, &
4325  18, 17, 13, &
4326  13, 14, 18, &
4327  19, 18, 14, &
4328  14, 15, 19, &
4329  20, 19, 15, &
4330  16, 17, 21, &
4331  22, 21, 17, &
4332  17, 18, 22, &
4333  23, 22, 18, &
4334  18, 19, 23, &
4335  24, 23, 19, &
4336  19, 20, 24, &
4337  25, 24, 20 /), (/ triangle_order, triangle_num /) )
4338 
4339  triangle_neighbor(1:3,1:triangle_num) = reshape( (/ &
4340  -1, 2, -1, &
4341  9, 1, 3, &
4342  -1, 4, 2, &
4343  11, 3, 5, &
4344  -1, 6, 4, &
4345  13, 5, 7, &
4346  -1, 8, 6, &
4347  15, 7, -1, &
4348  2, 10, -1, &
4349  17, 9, 11, &
4350  4, 12, 10, &
4351  19, 11, 13, &
4352  6, 14, 12, &
4353  21, 13, 15, &
4354  8, 16, 14, &
4355  23, 15, -1, &
4356  10, 18, -1, &
4357  25, 17, 19, &
4358  12, 20, 18, &
4359  27, 19, 21, &
4360  14, 22, 20, &
4361  29, 21, 23, &
4362  16, 24, 22, &
4363  31, 23, -1, &
4364  18, 26, -1, &
4365  -1, 25, 27, &
4366  20, 28, 26, &
4367  -1, 27, 29, &
4368  22, 30, 28, &
4369  -1, 29, 31, &
4370  24, 32, 30, &
4371  -1, 31, -1 /), (/ 3, triangle_num /) )
4372 
4373  return

◆ triangulation_order3_example2_size()

subroutine triangulation_order3_example2_size ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 )  hole_num 
)

Definition at line 4375 of file rcm.f90.

4377 
4378  !*****************************************************************************80
4379  !
4380  !! TRIANGULATION_ORDER3_EXAMPLE2_SIZE returns the size of an example.
4381  !
4382  ! Diagram:
4383  !
4384  ! 21-22-23-24-25
4385  ! |\ |\ |\ |\ |
4386  ! | \| \| \| \|
4387  ! 16-17-18-19-20
4388  ! |\ |\ |\ |\ |
4389  ! | \| \| \| \|
4390  ! 11-12-13-14-15
4391  ! |\ |\ |\ |\ |
4392  ! | \| \| \| \|
4393  ! 6--7--8--9-10
4394  ! |\ |\ |\ |\ |
4395  ! | \| \| \| \|
4396  ! 1--2--3--4--5
4397  !
4398  ! Licensing:
4399  !
4400  ! This code is distributed under the GNU LGPL license.
4401  !
4402  ! Modified:
4403  !
4404  ! 03 January 2007
4405  !
4406  ! Author:
4407  !
4408  ! John Burkardt
4409  !
4410  ! Parameters
4411  !
4412  ! Output, integer ( kind = 4 ) NODE_NUM, the number of nodes.
4413  !
4414  ! Output, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
4415  !
4416  ! Output, integer ( kind = 4 ) HOLE_NUM, the number of holes.
4417  !
4418  implicit none
4419 
4420  integer ( kind = 4 ) hole_num
4421  integer ( kind = 4 ) node_num
4422  integer ( kind = 4 ) triangle_num
4423 
4424  node_num = 25
4425  triangle_num = 32
4426  hole_num = 0
4427 
4428  return

◆ triangulation_order6_adj_count()

subroutine triangulation_order6_adj_count ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_col 
)

Definition at line 4430 of file rcm.f90.

4432 
4433  !*****************************************************************************80
4434  !
4435  !! TRIANGULATION_ORDER6_ADJ_COUNT counts adjacencies in a triangulation.
4436  !
4437  ! Discussion:
4438  !
4439  ! This routine is called to count the adjacencies, so that the
4440  ! appropriate amount of memory can be set aside for storage when
4441  ! the adjacency structure is created.
4442  !
4443  ! The triangulation is assumed to involve 6-node triangles.
4444  !
4445  ! Two nodes are "adjacent" if they are both nodes in some triangle.
4446  ! Also, a node is considered to be adjacent to itself.
4447  !
4448  ! Diagram:
4449  !
4450  ! 3
4451  ! s |\
4452  ! i | \
4453  ! d | \
4454  ! e 6 5 side 2
4455  ! | \
4456  ! 3 | \
4457  ! | \
4458  ! 1---4---2
4459  !
4460  ! side 1
4461  !
4462  ! The local node numbering
4463  !
4464  !
4465  ! 21-22-23-24-25
4466  ! |\ |\ |
4467  ! | \ | \ |
4468  ! 16 17 18 19 20
4469  ! | \ | \ |
4470  ! | \| \|
4471  ! 11-12-13-14-15
4472  ! |\ |\ |
4473  ! | \ | \ |
4474  ! 6 7 8 9 10
4475  ! | \ | \ |
4476  ! | \| \|
4477  ! 1--2--3--4--5
4478  !
4479  ! A sample grid.
4480  !
4481  !
4482  ! Below, we have a chart that lists the nodes adjacent to each node, with
4483  ! an asterisk to indicate the adjacency of the node to itself
4484  ! (in some cases, you want to count this self adjacency and in some
4485  ! you don't).
4486  !
4487  ! N Adjacencies
4488  !
4489  ! 1: * 2 3 6 7 11
4490  ! 2: 1 * 3 6 7 11
4491  ! 3: 1 2 * 4 5 6 7 8 9 11 12 13
4492  ! 4: 3 * 5 8 9 13
4493  ! 5: 3 4 * 8 9 10 13 14 15
4494  ! 6: 1 2 3 * 7 11
4495  ! 7: 1 2 3 6 * 8 11 12 13
4496  ! 8: 3 4 5 7 * 9 11 12 13
4497  ! 9: 3 4 5 8 * 10 13 14 15
4498  ! 10: 5 9 * 13 14 15
4499  ! 11: 1 2 3 6 7 8 * 12 13 16 17 21
4500  ! 12: 3 7 8 11 * 13 16 17 21
4501  ! 13: 3 4 5 7 8 9 10 11 12 * 14 15 16 17 18 19 21 22 23
4502  ! 14: 5 9 10 13 * 15 18 19 23
4503  ! 15: 5 9 10 13 14 * 18 19 20 23 24 25
4504  ! 16: 11 12 13 * 17 21
4505  ! 17: 11 12 13 16 * 18 21 22 23
4506  ! 18: 13 14 15 17 * 19 21 22 23
4507  ! 19: 13 14 15 18 * 20 23 24 25
4508  ! 20: 15 19 * 23 24 25
4509  ! 21: 11 12 13 16 17 18 * 22 23
4510  ! 22: 13 17 18 21 * 23
4511  ! 23: 13 14 15 17 18 19 20 21 22 * 24 25
4512  ! 24: 15 19 20 23 * 25
4513  ! 25: 15 19 20 23 24 *
4514  !
4515  ! Below, we list the number of adjacencies to lower-indexed nodes, to
4516  ! the node itself, to higher-indexed nodes, the total number of
4517  ! adjacencies for this node, and the location of the first and last
4518  ! entries required to list this set of adjacencies in a single list
4519  ! of all the adjacencies.
4520  !
4521  ! N Below Self Above Total First Last
4522  !
4523  ! -- -- -- -- -- --- 0
4524  ! 1: 0 1 5 6 1 6
4525  ! 2: 1 1 4 6 7 12
4526  ! 3: 2 1 9 12 13 24
4527  ! 4: 1 1 4 6 25 30
4528  ! 5: 2 1 6 9 31 39
4529  ! 6: 3 1 2 6 40 45
4530  ! 7: 4 1 4 9 46 54
4531  ! 8: 4 1 4 9 55 63
4532  ! 9: 4 1 4 9 62 72
4533  ! 10: 2 1 3 6 73 78
4534  ! 11: 6 1 5 12 79 90
4535  ! 12: 4 1 4 9 91 99
4536  ! 13: 9 1 9 19 100 118
4537  ! 14: 4 1 4 9 119 127
4538  ! 15: 5 1 6 12 128 139
4539  ! 16: 3 1 2 6 140 145
4540  ! 17: 4 1 4 9 146 154
4541  ! 18: 4 1 4 9 155 163
4542  ! 19: 4 1 4 9 164 172
4543  ! 20: 2 1 3 6 173 178
4544  ! 21: 6 1 2 9 179 187
4545  ! 22: 4 1 1 6 188 193
4546  ! 23: 9 1 2 12 194 205
4547  ! 24: 4 1 1 6 206 211
4548  ! 25: 5 1 0 6 212 217
4549  ! -- -- -- -- -- 218 ---
4550  !
4551  ! Licensing:
4552  !
4553  ! This code is distributed under the GNU LGPL license.
4554  !
4555  ! Modified:
4556  !
4557  ! 24 August 2006
4558  !
4559  ! Author:
4560  !
4561  ! John Burkardt
4562  !
4563  ! Parameters
4564  !
4565  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
4566  !
4567  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
4568  !
4569  ! Input, integer ( kind = 4 ) TRIANGLE_NODE(6,TRIANGLE_NUM), lists the nodes
4570  ! that make up each triangle. The first three nodes are the vertices,
4571  ! in counterclockwise order. The fourth value is the midside
4572  ! node between nodes 1 and 2; the fifth and sixth values are
4573  ! the other midside nodes in the logical order.
4574  !
4575  ! Input, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), for each
4576  ! side of a triangle, lists the neighboring triangle, or -1 if there is
4577  ! no neighbor.
4578  !
4579  ! Output, integer ( kind = 4 ) ADJ_NUM, the number of adjacencies.
4580  !
4581  ! Output, integer ( kind = 4 ) ADJ_COL(NODE_NUM+1). Information about
4582  ! column J is stored in entries ADJ_COL(J) through ADJ_COL(J+1)-1 of ADJ.
4583  !
4584  implicit none
4585 
4586  integer ( kind = 4 ) node_num
4587  integer ( kind = 4 ) triangle_num
4588  integer ( kind = 4 ), parameter :: triangle_order = 6
4589 
4590  integer ( kind = 4 ) adj_num
4591  integer ( kind = 4 ) adj_col(node_num+1)
4592  integer ( kind = 4 ) i
4593  integer ( kind = 4 ) n1
4594  integer ( kind = 4 ) n2
4595  integer ( kind = 4 ) n3
4596  integer ( kind = 4 ) n4
4597  integer ( kind = 4 ) n5
4598  integer ( kind = 4 ) n6
4599  integer ( kind = 4 ) triangle
4600  integer ( kind = 4 ) triangle2
4601  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
4602  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
4603 
4604  adj_num = 0
4605  !
4606  ! Set every node to be adjacent to itself.
4607  !
4608  adj_col(1:node_num) = 1
4609  !
4610  ! Examine each triangle.
4611  !
4612  do triangle = 1, triangle_num
4613 
4614  n1 = triangle_node(1,triangle)
4615  n2 = triangle_node(2,triangle)
4616  n3 = triangle_node(3,triangle)
4617  n4 = triangle_node(4,triangle)
4618  n5 = triangle_node(5,triangle)
4619  n6 = triangle_node(6,triangle)
4620  !
4621  ! For sure, we add the adjacencies:
4622  ! 43 / (34)
4623  ! 51 / (15)
4624  ! 54 / (45)
4625  ! 62 / (26)
4626  ! 64 / (46)
4627  ! 65 / (56)
4628  !
4629  adj_col(n3) = adj_col(n3) + 1
4630  adj_col(n4) = adj_col(n4) + 1
4631  adj_col(n1) = adj_col(n1) + 1
4632  adj_col(n5) = adj_col(n5) + 1
4633  adj_col(n4) = adj_col(n4) + 1
4634  adj_col(n5) = adj_col(n5) + 1
4635  adj_col(n2) = adj_col(n2) + 1
4636  adj_col(n6) = adj_col(n6) + 1
4637  adj_col(n4) = adj_col(n4) + 1
4638  adj_col(n6) = adj_col(n6) + 1
4639  adj_col(n5) = adj_col(n5) + 1
4640  adj_col(n6) = adj_col(n6) + 1
4641  !
4642  ! Add edges (1,2), (1,4), (2,4) if this is the first occurrence,
4643  ! that is, if the edge (1,4,2) is on a boundary (TRIANGLE2 <= 0)
4644  ! or if this triangle is the first of the pair in which the edge
4645  ! occurs (TRIANGLE < TRIANGLE2).
4646  !
4647  ! Maybe add
4648  ! 21 / 12
4649  ! 41 / 14
4650  ! 42 / 24
4651  !
4652  triangle2 = triangle_neighbor(1,triangle)
4653 
4654  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4655  adj_col(n1) = adj_col(n1) + 1
4656  adj_col(n2) = adj_col(n2) + 1
4657  adj_col(n1) = adj_col(n1) + 1
4658  adj_col(n4) = adj_col(n4) + 1
4659  adj_col(n2) = adj_col(n2) + 1
4660  adj_col(n4) = adj_col(n4) + 1
4661  end if
4662  !
4663  ! Maybe add
4664  ! 32 / 23
4665  ! 52 / 25
4666  ! 53 / 35
4667  !
4668  triangle2 = triangle_neighbor(2,triangle)
4669 
4670  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4671  adj_col(n2) = adj_col(n2) + 1
4672  adj_col(n3) = adj_col(n3) + 1
4673  adj_col(n2) = adj_col(n2) + 1
4674  adj_col(n5) = adj_col(n5) + 1
4675  adj_col(n3) = adj_col(n3) + 1
4676  adj_col(n5) = adj_col(n5) + 1
4677  end if
4678  !
4679  ! Maybe add
4680  ! 31 / 13
4681  ! 61 / 16
4682  ! 63 / 36
4683  !
4684  triangle2 = triangle_neighbor(3,triangle)
4685 
4686  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4687  adj_col(n1) = adj_col(n1) + 1
4688  adj_col(n3) = adj_col(n3) + 1
4689  adj_col(n1) = adj_col(n1) + 1
4690  adj_col(n6) = adj_col(n6) + 1
4691  adj_col(n3) = adj_col(n3) + 1
4692  adj_col(n6) = adj_col(n6) + 1
4693  end if
4694 
4695  end do
4696  !
4697  ! We used ADJ_COL to count the number of entries in each column.
4698  ! Convert it to pointers into the ADJ array.
4699  !
4700  adj_col(2:node_num+1) = adj_col(1:node_num)
4701 
4702  adj_col(1) = 1
4703  do i = 2, node_num + 1
4704  adj_col(i) = adj_col(i-1) + adj_col(i)
4705  end do
4706 
4707  adj_num = adj_col(node_num+1) - 1
4708 
4709  return

◆ triangulation_order6_adj_set()

subroutine triangulation_order6_adj_set ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor,
integer ( kind = 4 )  adj_num,
integer ( kind = 4 ), dimension(node_num+1)  adj_col,
integer ( kind = 4 ), dimension(adj_num)  adj 
)

Definition at line 4711 of file rcm.f90.

4713 
4714  !*****************************************************************************80
4715  !
4716  !! TRIANGULATION_ORDER6_ADJ_SET sets adjacencies in a triangulation.
4717  !
4718  ! Discussion:
4719  !
4720  ! This routine is called to count the adjacencies, so that the
4721  ! appropriate amount of memory can be set aside for storage when
4722  ! the adjacency structure is created.
4723  !
4724  ! The triangulation is assumed to involve 6-node triangles.
4725  !
4726  ! Two nodes are "adjacent" if they are both nodes in some triangle.
4727  ! Also, a node is considered to be adjacent to itself.
4728  !
4729  ! This routine can be used to create the compressed column storage
4730  ! for a quadratic triangle finite element discretization of
4731  ! Poisson's equation in two dimensions.
4732  !
4733  ! Diagram:
4734  !
4735  ! 3
4736  ! s |\
4737  ! i | \
4738  ! d | \
4739  ! e 6 5 side 2
4740  ! | \
4741  ! 3 | \
4742  ! | \
4743  ! 1---4---2
4744  !
4745  ! side 1
4746  !
4747  ! The local node numbering
4748  !
4749  !
4750  ! 21-22-23-24-25
4751  ! |\ |\ |
4752  ! | \ | \ |
4753  ! 16 17 18 19 20
4754  ! | \ | \ |
4755  ! | \| \|
4756  ! 11-12-13-14-15
4757  ! |\ |\ |
4758  ! | \ | \ |
4759  ! 6 7 8 9 10
4760  ! | \ | \ |
4761  ! | \| \|
4762  ! 1--2--3--4--5
4763  !
4764  ! A sample grid.
4765  !
4766  !
4767  ! Below, we have a chart that lists the nodes adjacent to each node, with
4768  ! an asterisk to indicate the adjacency of the node to itself
4769  ! (in some cases, you want to count this self adjacency and in some
4770  ! you don't).
4771  !
4772  ! N Adjacencies
4773  !
4774  ! 1: * 2 3 6 7 11
4775  ! 2: 1 * 3 6 7 11
4776  ! 3: 1 2 * 4 5 6 7 8 9 11 12 13
4777  ! 4: 3 * 5 8 9 13
4778  ! 5: 3 4 * 8 9 10 13 14 15
4779  ! 6: 1 2 3 * 7 11
4780  ! 7: 1 2 3 6 * 8 11 12 13
4781  ! 8: 3 4 5 7 * 9 11 12 13
4782  ! 9: 3 4 5 8 * 10 13 14 15
4783  ! 10: 5 9 * 13 14 15
4784  ! 11: 1 2 3 6 7 8 * 12 13 16 17 21
4785  ! 12: 3 7 8 11 * 13 16 17 21
4786  ! 13: 3 4 5 7 8 9 10 11 12 * 14 15 16 17 18 19 21 22 23
4787  ! 14: 5 9 10 13 * 15 18 19 23
4788  ! 15: 5 9 10 13 14 * 18 19 20 23 24 25
4789  ! 16: 11 12 13 * 17 21
4790  ! 17: 11 12 13 16 * 18 21 22 23
4791  ! 18: 13 14 15 17 * 19 21 22 23
4792  ! 19: 13 14 15 18 * 20 23 24 25
4793  ! 20: 15 19 * 23 24 25
4794  ! 21: 11 12 13 16 17 18 * 22 23
4795  ! 22: 13 17 18 21 * 23
4796  ! 23: 13 14 15 17 18 19 20 21 22 * 24 25
4797  ! 24: 15 19 20 23 * 25
4798  ! 25: 15 19 20 23 24 *
4799  !
4800  ! Below, we list the number of adjacencies to lower-indexed nodes, to
4801  ! the node itself, to higher-indexed nodes, the total number of
4802  ! adjacencies for this node, and the location of the first and last
4803  ! entries required to list this set of adjacencies in a single list
4804  ! of all the adjacencies.
4805  !
4806  ! N Below Self Above Total First Last
4807  !
4808  ! -- -- -- -- -- --- 0
4809  ! 1: 0 1 5 6 1 6
4810  ! 2: 1 1 4 6 7 12
4811  ! 3: 2 1 9 12 13 24
4812  ! 4: 1 1 4 6 25 30
4813  ! 5: 2 1 6 9 31 39
4814  ! 6: 3 1 2 6 40 45
4815  ! 7: 4 1 4 9 46 54
4816  ! 8: 4 1 4 9 55 63
4817  ! 9: 4 1 4 9 62 72
4818  ! 10: 2 1 3 6 73 78
4819  ! 11: 6 1 5 12 79 90
4820  ! 12: 4 1 4 9 91 99
4821  ! 13: 9 1 9 19 100 118
4822  ! 14: 4 1 4 9 119 127
4823  ! 15: 5 1 6 12 128 139
4824  ! 16: 3 1 2 6 140 145
4825  ! 17: 4 1 4 9 146 154
4826  ! 18: 4 1 4 9 155 163
4827  ! 19: 4 1 4 9 164 172
4828  ! 20: 2 1 3 6 173 178
4829  ! 21: 6 1 2 9 179 187
4830  ! 22: 4 1 1 6 188 193
4831  ! 23: 9 1 2 12 194 205
4832  ! 24: 4 1 1 6 206 211
4833  ! 25: 5 1 0 6 212 217
4834  ! -- -- -- -- -- 218 ---
4835  !
4836  ! Licensing:
4837  !
4838  ! This code is distributed under the GNU LGPL license.
4839  !
4840  ! Modified:
4841  !
4842  ! 24 August 2006
4843  !
4844  ! Author:
4845  !
4846  ! John Burkardt
4847  !
4848  ! Parameters
4849  !
4850  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
4851  !
4852  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
4853  !
4854  ! Input, integer ( kind = 4 ) TRIANGLE_NODE(6,TRIANGLE_NUM), lists the nodes
4855  ! that make up each triangle. The first three nodes are the vertices,
4856  ! in counterclockwise order. The fourth value is the midside
4857  ! node between nodes 1 and 2; the fifth and sixth values are
4858  ! the other midside nodes in the logical order.
4859  !
4860  ! Input, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), for each
4861  ! side of a triangle, lists the neighboring triangle, or -1 if there is
4862  ! no neighbor.
4863  !
4864  ! Input, integer ( kind = 4 ) ADJ_NUM, the number of adjacencies.
4865  !
4866  ! Input, integer ( kind = 4 ) ADJ_COL(NODE_NUM+1). Information about
4867  ! column J is stored in entries ADJ_COL(J) through ADJ_COL(J+1)-1 of ADJ.
4868  !
4869  ! Output, integer ( kind = 4 ) ADJ(ADJ_NUM), the adjacency information.
4870  !
4871  implicit none
4872 
4873  integer ( kind = 4 ) adj_num
4874  integer ( kind = 4 ) node_num
4875  integer ( kind = 4 ) triangle_num
4876  integer ( kind = 4 ), parameter :: triangle_order = 6
4877 
4878  integer ( kind = 4 ) adj(adj_num)
4879  integer ( kind = 4 ) adj_copy(node_num)
4880  integer ( kind = 4 ) adj_col(node_num+1)
4881  integer ( kind = 4 ) k1
4882  integer ( kind = 4 ) k2
4883  integer ( kind = 4 ) n1
4884  integer ( kind = 4 ) n2
4885  integer ( kind = 4 ) n3
4886  integer ( kind = 4 ) n4
4887  integer ( kind = 4 ) n5
4888  integer ( kind = 4 ) n6
4889  integer ( kind = 4 ) node
4890  integer ( kind = 4 ) triangle
4891  integer ( kind = 4 ) triangle2
4892  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
4893  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
4894 
4895  adj(1:adj_num) = -1
4896  adj_copy(1:node_num) = adj_col(1:node_num)
4897  !
4898  ! Set every node to be adjacent to itself.
4899  !
4900  do node = 1, node_num
4901  adj(adj_copy(node)) = node
4902  adj_copy(node) = adj_copy(node) + 1
4903  end do
4904  !
4905  ! Examine each triangle.
4906  !
4907  do triangle = 1, triangle_num
4908 
4909  n1 = triangle_node(1,triangle)
4910  n2 = triangle_node(2,triangle)
4911  n3 = triangle_node(3,triangle)
4912  n4 = triangle_node(4,triangle)
4913  n5 = triangle_node(5,triangle)
4914  n6 = triangle_node(6,triangle)
4915  !
4916  ! For sure, we add the adjacencies:
4917  ! 43 / (34)
4918  ! 51 / (15)
4919  ! 54 / (45)
4920  ! 62 / (26)
4921  ! 64 / (46)
4922  ! 65 / (56)
4923  !
4924  adj(adj_copy(n3)) = n4
4925  adj_copy(n3) = adj_copy(n3) + 1
4926  adj(adj_copy(n4)) = n3
4927  adj_copy(n4) = adj_copy(n4) + 1
4928 
4929  adj(adj_copy(n1)) = n5
4930  adj_copy(n1) = adj_copy(n1) + 1
4931  adj(adj_copy(n5)) = n1
4932  adj_copy(n5) = adj_copy(n5) + 1
4933 
4934  adj(adj_copy(n4)) = n5
4935  adj_copy(n4) = adj_copy(n4) + 1
4936  adj(adj_copy(n5)) = n4
4937  adj_copy(n5) = adj_copy(n5) + 1
4938 
4939  adj(adj_copy(n2)) = n6
4940  adj_copy(n2) = adj_copy(n2) + 1
4941  adj(adj_copy(n6)) = n2
4942  adj_copy(n6) = adj_copy(n6) + 1
4943 
4944  adj(adj_copy(n4)) = n6
4945  adj_copy(n4) = adj_copy(n4) + 1
4946  adj(adj_copy(n6)) = n4
4947  adj_copy(n6) = adj_copy(n6) + 1
4948 
4949  adj(adj_copy(n5)) = n6
4950  adj_copy(n5) = adj_copy(n5) + 1
4951  adj(adj_copy(n6)) = n5
4952  adj_copy(n6) = adj_copy(n6) + 1
4953  !
4954  ! Add edges (1,2), (1,4), (2,4) if this is the first occurrence,
4955  ! that is, if the edge (1,4,2) is on a boundary (TRIANGLE2 <= 0)
4956  ! or if this triangle is the first of the pair in which the edge
4957  ! occurs (TRIANGLE < TRIANGLE2).
4958  !
4959  ! Maybe add
4960  ! 21 / 12
4961  ! 41 / 14
4962  ! 42 / 24
4963  !
4964  triangle2 = triangle_neighbor(1,triangle)
4965 
4966  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4967  adj(adj_copy(n1)) = n2
4968  adj_copy(n1) = adj_copy(n1) + 1
4969  adj(adj_copy(n2)) = n1
4970  adj_copy(n2) = adj_copy(n2) + 1
4971  adj(adj_copy(n1)) = n4
4972  adj_copy(n1) = adj_copy(n1) + 1
4973  adj(adj_copy(n4)) = n1
4974  adj_copy(n4) = adj_copy(n4) + 1
4975  adj(adj_copy(n2)) = n4
4976  adj_copy(n2) = adj_copy(n2) + 1
4977  adj(adj_copy(n4)) = n2
4978  adj_copy(n4) = adj_copy(n4) + 1
4979  end if
4980  !
4981  ! Maybe add
4982  ! 32 / 23
4983  ! 52 / 25
4984  ! 53 / 35
4985  !
4986  triangle2 = triangle_neighbor(2,triangle)
4987 
4988  if ( triangle2 < 0 .or. triangle < triangle2 ) then
4989  adj(adj_copy(n2)) = n3
4990  adj_copy(n2) = adj_copy(n2) + 1
4991  adj(adj_copy(n3)) = n2
4992  adj_copy(n3) = adj_copy(n3) + 1
4993  adj(adj_copy(n2)) = n5
4994  adj_copy(n2) = adj_copy(n2) + 1
4995  adj(adj_copy(n5)) = n2
4996  adj_copy(n5) = adj_copy(n5) + 1
4997  adj(adj_copy(n3)) = n5
4998  adj_copy(n3) = adj_copy(n3) + 1
4999  adj(adj_copy(n5)) = n3
5000  adj_copy(n5) = adj_copy(n5) + 1
5001  end if
5002  !
5003  ! Maybe add
5004  ! 31 / 13
5005  ! 61 / 16
5006  ! 63 / 36
5007  !
5008  triangle2 = triangle_neighbor(3,triangle)
5009 
5010  if ( triangle2 < 0 .or. triangle < triangle2 ) then
5011  adj(adj_copy(n1)) = n3
5012  adj_copy(n1) = adj_copy(n1) + 1
5013  adj(adj_copy(n3)) = n1
5014  adj_copy(n3) = adj_copy(n3) + 1
5015  adj(adj_copy(n1)) = n6
5016  adj_copy(n1) = adj_copy(n1) + 1
5017  adj(adj_copy(n6)) = n1
5018  adj_copy(n6) = adj_copy(n6) + 1
5019  adj(adj_copy(n3)) = n6
5020  adj_copy(n3) = adj_copy(n3) + 1
5021  adj(adj_copy(n6)) = n3
5022  adj_copy(n6) = adj_copy(n6) + 1
5023  end if
5024 
5025  end do
5026  !
5027  ! Ascending sort the entries for each node.
5028  !
5029  do node = 1, node_num
5030  k1 = adj_col(node)
5031  k2 = adj_col(node+1)-1
5032  call i4vec_sort_heap_a ( k2+1-k1, adj(k1:k2) )
5033  end do
5034 
5035  return
Here is the call graph for this function:

◆ triangulation_order6_example2()

subroutine triangulation_order6_example2 ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
real ( kind = 8 ), dimension(dim_num,node_num)  node_xy,
integer ( kind = 4 ), dimension(triangle_order,triangle_num)  triangle_node,
integer ( kind = 4 ), dimension(3,triangle_num)  triangle_neighbor 
)

Definition at line 5037 of file rcm.f90.

5039 
5040  !*****************************************************************************80
5041  !
5042  !! TRIANGULATION_ORDER6_EXAMPLE2 returns an example triangulation.
5043  !
5044  ! Discussion:
5045  !
5046  ! This triangulation is actually a Delaunay triangulation.
5047  !
5048  ! The appropriate input values of NODE_NUM and TRIANGLE_NUM can be
5049  ! determined by calling TRIANGULATION_ORDER6_EXAMPLE2_SIZE first.
5050  !
5051  ! Diagram:
5052  !
5053  ! 21-22-23-24-25
5054  ! |\ 6 |\ 8 |
5055  ! | \ | \ |
5056  ! 16 17 18 19 20
5057  ! | \ | \ |
5058  ! | 5 \| 7 \|
5059  ! 11-12-13-14-15
5060  ! |\ 2 |\ 4 |
5061  ! | \ | \ |
5062  ! 6 7 8 9 10
5063  ! | 1 \ | 3 \ |
5064  ! | \| \|
5065  ! 1--2--3--4--5
5066  !
5067  ! Licensing:
5068  !
5069  ! This code is distributed under the GNU LGPL license.
5070  !
5071  ! Modified:
5072  !
5073  ! 03 January 2007
5074  !
5075  ! Author:
5076  !
5077  ! John Burkardt
5078  !
5079  ! Parameters
5080  !
5081  ! Input, integer ( kind = 4 ) NODE_NUM, the number of nodes.
5082  !
5083  ! Input, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
5084  !
5085  ! Output, real ( kind = 8 ) NODE_XY(2,NODE_NUM), the coordinates of
5086  ! the nodes.
5087  !
5088  ! Output, integer ( kind = 4 ) TRIANGLE_NODE(6,TRIANGLE_NUM), lists the
5089  ! nodes that make up each triangle. The first three nodes are the vertices,
5090  ! in counterclockwise order. The fourth value is the midside
5091  ! node between nodes 1 and 2; the fifth and sixth values are
5092  ! the other midside nodes in the logical order.
5093  !
5094  ! Output, integer ( kind = 4 ) TRIANGLE_NEIGHBOR(3,TRIANGLE_NUM), for each
5095  ! side of a triangle, lists the neighboring triangle, or -1 if there is
5096  ! no neighbor.
5097  !
5098  implicit none
5099 
5100  integer ( kind = 4 ), parameter :: dim_num = 2
5101  integer ( kind = 4 ) node_num
5102  integer ( kind = 4 ) triangle_num
5103  integer ( kind = 4 ), parameter :: triangle_order = 6
5104 
5105  real ( kind = 8 ) node_xy(dim_num,node_num)
5106  integer ( kind = 4 ) triangle_neighbor(3,triangle_num)
5107  integer ( kind = 4 ) triangle_node(triangle_order,triangle_num)
5108 
5109  node_xy = reshape( (/ &
5110  0.0d+00, 0.0d+00, &
5111  1.0d+00, 0.0d+00, &
5112  2.0d+00, 0.0d+00, &
5113  3.0d+00, 0.0d+00, &
5114  4.0d+00, 0.0d+00, &
5115  0.0d+00, 1.0d+00, &
5116  1.0d+00, 1.0d+00, &
5117  2.0d+00, 1.0d+00, &
5118  3.0d+00, 1.0d+00, &
5119  4.0d+00, 1.0d+00, &
5120  0.0d+00, 2.0d+00, &
5121  1.0d+00, 2.0d+00, &
5122  2.0d+00, 2.0d+00, &
5123  3.0d+00, 2.0d+00, &
5124  4.0d+00, 2.0d+00, &
5125  0.0d+00, 3.0d+00, &
5126  1.0d+00, 3.0d+00, &
5127  2.0d+00, 3.0d+00, &
5128  3.0d+00, 3.0d+00, &
5129  4.0d+00, 3.0d+00, &
5130  0.0d+00, 4.0d+00, &
5131  1.0d+00, 4.0d+00, &
5132  2.0d+00, 4.0d+00, &
5133  3.0d+00, 4.0d+00, &
5134  4.0d+00, 4.0d+00 &
5135  /), (/ dim_num, node_num /) )
5136 
5137  triangle_node(1:triangle_order,1:triangle_num) = reshape( (/ &
5138  1, 3, 11, 2, 7, 6, &
5139  13, 11, 3, 12, 7, 8, &
5140  3, 5, 13, 4, 9, 8, &
5141  15, 13, 5, 14, 9, 10, &
5142  11, 13, 21, 12, 17, 16, &
5143  23, 21, 13, 22, 17, 18, &
5144  13, 15, 23, 14, 19, 18, &
5145  25, 23, 15, 24, 19, 20 /), (/ triangle_order, triangle_num /) )
5146 
5147  triangle_neighbor(1:3,1:triangle_num) = reshape( (/ &
5148  -1, 2, -1, &
5149  5, 1, 3, &
5150  -1, 4, 2, &
5151  7, 3, -1, &
5152  2, 6, -1, &
5153  -1, 5, 7, &
5154  4, 8, 6, &
5155  -1, 7, -1 /), (/ 3, triangle_num /) )
5156 
5157  return

◆ triangulation_order6_example2_size()

subroutine triangulation_order6_example2_size ( integer ( kind = 4 )  node_num,
integer ( kind = 4 )  triangle_num,
integer ( kind = 4 )  hole_num 
)

Definition at line 5159 of file rcm.f90.

5161 
5162  !*****************************************************************************80
5163  !
5164  !! TRIANGULATION_ORDER6_EXAMPLE2_SIZE returns the size of an example.
5165  !
5166  ! Diagram:
5167  !
5168  ! 21-22-23-24-25
5169  ! |\ 6 |\ 8 |
5170  ! | \ | \ |
5171  ! 16 17 18 19 20
5172  ! | \ | \ |
5173  ! | 5 \| 7 \|
5174  ! 11-12-13-14-15
5175  ! |\ 2 |\ 4 |
5176  ! | \ | \ |
5177  ! 6 7 8 9 10
5178  ! | 1 \ | 3 \ |
5179  ! | \| \|
5180  ! 1--2--3--4--5
5181  !
5182  ! Licensing:
5183  !
5184  ! This code is distributed under the GNU LGPL license.
5185  !
5186  ! Modified:
5187  !
5188  ! 03 January 2007
5189  !
5190  ! Author:
5191  !
5192  ! John Burkardt
5193  !
5194  ! Parameters
5195  !
5196  ! Output, integer ( kind = 4 ) NODE_NUM, the number of nodes.
5197  !
5198  ! Output, integer ( kind = 4 ) TRIANGLE_NUM, the number of triangles.
5199  !
5200  ! Output, integer ( kind = 4 ) HOLE_NUM, the number of holes.
5201  !
5202  implicit none
5203 
5204  integer ( kind = 4 ) hole_num
5205  integer ( kind = 4 ) node_num
5206  integer ( kind = 4 ) triangle_num
5207 
5208  node_num = 25
5209  triangle_num = 8
5210  hole_num = 0
5211 
5212  return