leastsquaresgradientmodule Module Reference

Data Types
type	array2d
interface	leastsquaresgradienttype
	Weighted least-squares gradient method for structured and unstructured grids. More...

Functions/Subroutines
type(leastsquaresgradienttype) function	constructor (dis)
real(dp) function, dimension(:, :), allocatable	create_gradient_reconstruction_matrix (this, n)
real(dp) function, dimension(3)	get (this, n)
subroutine	set_field (this, phi)
real(dp) function, dimension(3)	compute_cell_gradient (this, n)

Function/Subroutine Documentation

compute_cell_gradient()

real(dp) function, dimension(3) leastsquaresgradientmodule::compute_cell_gradient ( class(leastsquaresgradienttype), target  this, integer(i4b), intent(in)  n  )

private

Definition at line 140 of file LeastSquaresGradient.f90.

    ! -- return
    real(DP), dimension(3) :: grad_c
    ! -- dummy
    class(LeastSquaresGradientType), target :: this
    integer(I4B), intent(in) :: n
    ! -- local
    real(DP), dimension(:, :), pointer :: R
    integer(I4B) :: ipos, local_pos
    integer(I4B) :: number_connections
 
    integer(I4B) :: m
    real(DP), dimension(:), allocatable :: dc
 
    ! Assemble the concentration difference vector
    number_connections = number_connected_faces(this%dis, n)
    allocate (dc(number_connections))
    local_pos = 1
    do ipos = this%dis%con%ia(n) + 1, this%dis%con%ia(n + 1) - 1
      m = this%dis%con%ja(ipos)
      dc(local_pos) = this%phi(m) - this%phi(n)
      local_pos = local_pos + 1
    end do
 
    ! Compute the cells gradient
    r => this%R(n)%data
    grad_c = matmul(r, dc)
 

Here is the call graph for this function:

constructor()

type(leastsquaresgradienttype) function leastsquaresgradientmodule::constructor ( class(disbasetype), intent(in), pointer  dis )

private

Definition at line 60 of file LeastSquaresGradient.f90.

    ! --dummy
    class(DisBaseType), pointer, intent(in) :: dis
    !-- return
    type(LeastSquaresGradientType) :: gradient
    ! -- local
    integer(I4B) :: n, nodes
 
    gradient%dis => dis
    nodes = dis%nodes
 
    ! -- Compute the gradient rec
    nodes = dis%nodes
    allocate (gradient%R(dis%nodes))
    do n = 1, nodes
      gradient%R(n)%data = gradient%create_gradient_reconstruction_matrix(n)
    end do

Here is the caller graph for this function:

create_gradient_reconstruction_matrix()

real(dp) function, dimension(:, :), allocatable leastsquaresgradientmodule::create_gradient_reconstruction_matrix ( class(leastsquaresgradienttype)  this, integer(i4b), intent(in)  n  )

private

Definition at line 79 of file LeastSquaresGradient.f90.

    ! -- dummy
    class(LeastSquaresGradientType) :: this
    integer(I4B), intent(in) :: n ! Cell index for which to create the operator
    real(DP), dimension(:, :), allocatable :: R ! The resulting gradient reconstruction matrix (3 x number_connections)
    ! -- local
    integer(I4B) :: number_connections ! Number of connected neighboring cells
    integer(I4B) :: ipos, local_pos, m ! Loop indices and neighbor cell index
    real(DP) :: length ! Distance between cell centers
    real(DP), dimension(3) :: dnm ! Vector from cell n to neighbor m
    real(DP), dimension(:, :), allocatable :: d ! Matrix of normalized direction vectors (number_connections x 3)
    real(DP), dimension(:, :), allocatable :: inverse_distance ! Diagonal scaling matrix (number_connections x number_connections),
    ! where each diagonal entry is the inverse of the distance between
 
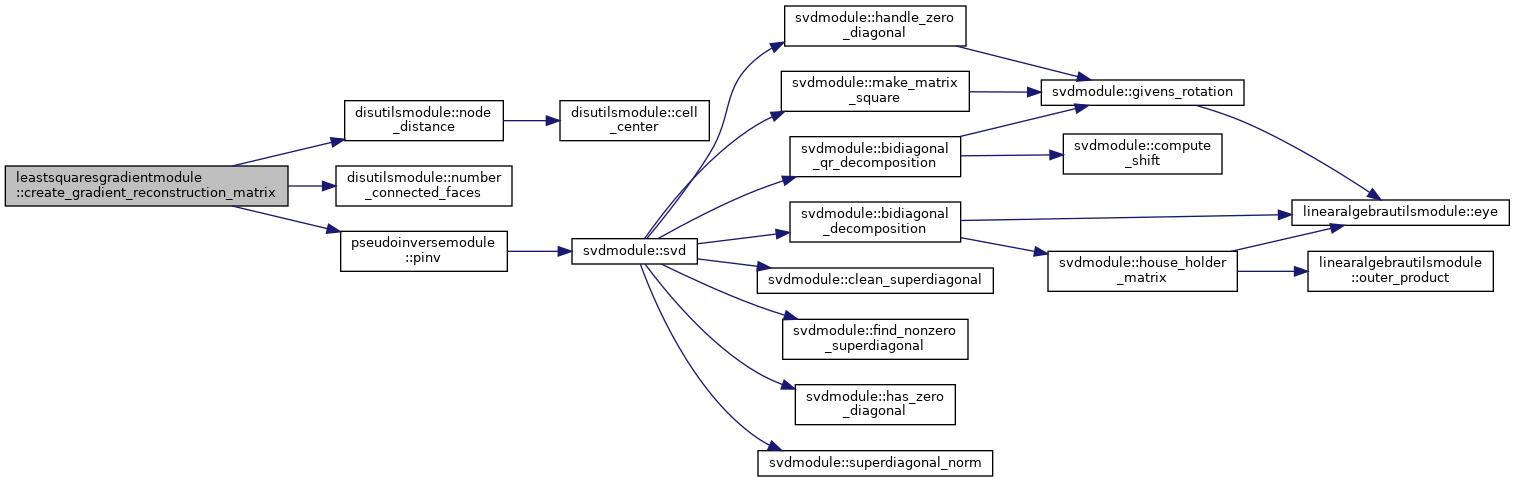
    number_connections = number_connected_faces(this%dis, n)
 
    allocate (d(number_connections, 3))
    allocate (r(3, number_connections))
    allocate (inverse_distance(number_connections, number_connections))
 
    inverse_distance = 0
    d = 0
 
    ! Assemble the distance matrix
    ! Handle the internal connections
    local_pos = 1
    do ipos = this%dis%con%ia(n) + 1, this%dis%con%ia(n + 1) - 1
      m = this%dis%con%ja(ipos)
 
      dnm = node_distance(this%dis, n, m)
      length = norm2(dnm)
 
      d(local_pos, :) = dnm / length
      inverse_distance(local_pos, local_pos) = 1.0_dp / length
 
      local_pos = local_pos + 1
    end do
 
    ! Compute the gradient reconstructions matrix
    r = matmul(pinv(d), inverse_distance)
 

Here is the call graph for this function:

get()

real(dp) function, dimension(3) leastsquaresgradientmodule::get ( class(leastsquaresgradienttype), target  this, integer(i4b), intent(in)  n  )

private

Definition at line 122 of file LeastSquaresGradient.f90.

    ! -- dummy
    class(LeastSquaresGradientType), target :: this
    integer(I4B), intent(in) :: n
    !-- return
    real(DP), dimension(3) :: grad_c
 
    grad_c = this%compute_cell_gradient(n)

set_field()

subroutine leastsquaresgradientmodule::set_field ( class(leastsquaresgradienttype), target  this, real(dp), dimension(:), intent(in), pointer  phi  )

private

Definition at line 132 of file LeastSquaresGradient.f90.

    ! -- dummy
    class(LeastSquaresGradientType), target :: this
    real(DP), dimension(:), pointer, intent(in) :: phi
 
    this%phi => phi