leastsquaresgradientmodule::leastsquaresgradienttype Interface Reference

Weighted least-squares gradient method for structured and unstructured grids. More...

Inheritance diagram for leastsquaresgradientmodule::leastsquaresgradienttype:

Collaboration diagram for leastsquaresgradientmodule::leastsquaresgradienttype:

Private Member Functions
procedure	get
procedure	set_field
procedure, private	compute_cell_gradient
procedure, private	create_gradient_reconstruction_matrix
type(leastsquaresgradienttype) function	constructor (dis)

Private Attributes
class(disbasetype), pointer	dis
real(dp), dimension(:), pointer	phi
type(array2d), dimension(:), allocatable	r

Detailed Description

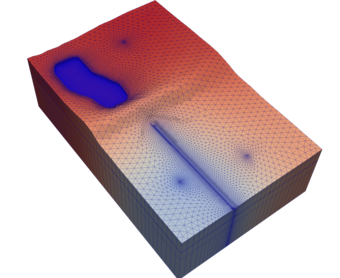
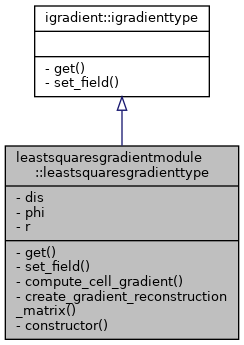
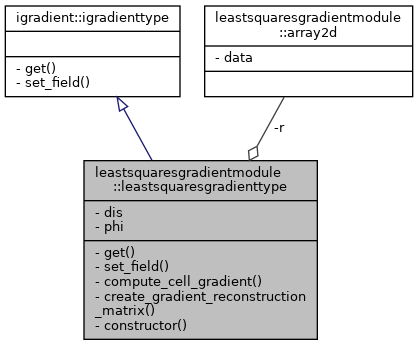
This class implements a least-squares gradient reconstruction for use on both structured and unstructured grids. For each cell, it precomputes and caches a gradient reconstruction matrix using the Moore-Penrose pseudoinverse, based on the geometry and connectivity of the mesh. The operator is created once during initialization and can then be efficiently applied to any scalar field to compute the gradient in each cell. The gradient can then be computed by multiplying the reconstruction matrix with the difference vector. ∇ɸ = R * ∑(ɸ_i - ɸ_up), where i are the neighboring cells.

Usage:

1. Create the gradient object with the discretization
2. Set the scalar field using set_field(phi) where phi is the field for which gradients are computed
3. Retrieve gradients for any cell using the get(n) method

• The gradient operator is constructed using normalized direction vectors between cell centers, scaled by the inverse of the distance.
• The least-squares approach ensures robust gradients even for irregular or rank-deficient stencils.
• The operator is cached for each cell, so gradient computation is efficient for repeated queries.
• The set_field method establishes a pointer to the scalar field data.
• The get method computes the gradient for any cell using the current scalar field.

Note

Boundary cells are not handled in a special manner. This may impact the quality of the gradient near boundaries, especially if a cell does not have enough neighbors (fewer than three in 3D).

Definition at line 43 of file LeastSquaresGradient.f90.

Member Function/Subroutine Documentation

compute_cell_gradient()

procedure, private leastsquaresgradientmodule::leastsquaresgradienttype::compute_cell_gradient

private

Definition at line 51 of file LeastSquaresGradient.f90.

constructor()

type(leastsquaresgradienttype) function leastsquaresgradientmodule::leastsquaresgradienttype::constructor ( class(disbasetype), intent(in), pointer  dis )

private

Definition at line 60 of file LeastSquaresGradient.f90.

    ! --dummy
    class(DisBaseType), pointer, intent(in) :: dis
    !-- return
    type(LeastSquaresGradientType) :: gradient
    ! -- local
    integer(I4B) :: n, nodes
 
    gradient%dis => dis
    nodes = dis%nodes
 
    ! -- Compute the gradient rec
    nodes = dis%nodes
    allocate (gradient%R(dis%nodes))
    do n = 1, nodes
      gradient%R(n)%data = gradient%create_gradient_reconstruction_matrix(n)
    end do

create_gradient_reconstruction_matrix()

procedure, private leastsquaresgradientmodule::leastsquaresgradienttype::create_gradient_reconstruction_matrix

private

Definition at line 52 of file LeastSquaresGradient.f90.

Here is the call graph for this function:

get()

procedure leastsquaresgradientmodule::leastsquaresgradienttype::get

private

Definition at line 48 of file LeastSquaresGradient.f90.

set_field()

procedure leastsquaresgradientmodule::leastsquaresgradienttype::set_field

private

Definition at line 49 of file LeastSquaresGradient.f90.

Member Data Documentation

dis

class(disbasetype), pointer leastsquaresgradientmodule::leastsquaresgradienttype::dis

private

Definition at line 44 of file LeastSquaresGradient.f90.

    class(DisBaseType), pointer :: dis

phi

real(dp), dimension(:), pointer leastsquaresgradientmodule::leastsquaresgradienttype::phi

private

Definition at line 45 of file LeastSquaresGradient.f90.

    real(DP), dimension(:), pointer :: phi

r

type(array2d), dimension(:), allocatable leastsquaresgradientmodule::leastsquaresgradienttype::r

private

Definition at line 46 of file LeastSquaresGradient.f90.

    type(Array2D), allocatable, dimension(:) :: R ! Gradient reconstruction matrix

---

The documentation for this interface was generated from the following file:

• /home/runner/work/modflow6/modflow6/src/Model/TransportModel/Gradient/LeastSquaresGradient.f90